欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
# 动态规划:目标和!难度:中等
给定一个非负整数数组,a1, a2, ..., an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例:
输入:nums: [1, 1, 1, 1, 1], S: 3
输出:5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
提示:
- 数组非空,且长度不会超过 20 。
- 初始的数组的和不会超过 1000 。
- 保证返回的最终结果能被 32 位整数存下。
如果跟着「代码随想录」一起学过回溯算法系列的录友,看到这道题,应该有一种直觉,就是感觉好像回溯法可以爆搜出来。
事实确实如此,下面我也会给出相应的代码,只不过会超时,哈哈。
这道题目咋眼一看和动态规划背包啥的也没啥关系。
本题要如何使表达式结果为target,
既然为target,那么就一定有 left组合 - right组合 = target。
left + right等于sum,而sum是固定的。
公式来了, left - (sum - left) = target -> left = (target + sum)/2 。
target是固定的,sum是固定的,left就可以求出来。
此时问题就是在集合nums中找出和为left的组合。
在回溯算法系列中,一起学过这道题目回溯算法:39. 组合总和的录友应该感觉很熟悉,这不就是组合总和问题么?
此时可以套组合总和的回溯法代码,几乎不用改动。
当然,也可以转变成序列区间选+ 或者 -,使用回溯法,那就是另一个解法。
我也把代码给出来吧,大家可以了解一下,回溯的解法,以下是本题转变为组合总和问题的回溯法代码:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
if (sum == target) {
result.push_back(path);
}
// 如果 sum + candidates[i] > target 就终止遍历
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i + 1);
sum -= candidates[i];
path.pop_back();
}
}
public:
int findTargetSumWays(vector<int>& nums, int S) {
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
if (S > sum) return 0; // 此时没有方案
if ((S + sum) % 2) return 0; // 此时没有方案,两个int相加的时候要各位小心数值溢出的问题
int bagSize = (S + sum) / 2; // 转变为组合总和问题,bagsize就是要求的和
// 以下为回溯法代码
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 需要排序
backtracking(nums, bagSize, 0, 0);
return result.size();
}
};当然以上代码超时了。
也可以使用记忆化回溯,但这里我就不在回溯上下功夫了,直接看动规吧
如何转化为01背包问题呢。
假设加法的总和为x,那么减法对应的总和就是sum - x。
所以我们要求的是 x - (sum - x) = S
x = (S + sum) / 2
此时问题就转化为,装满容量为x背包,有几种方法。
大家看到(S + sum) / 2 应该担心计算的过程中向下取整有没有影响。
这么担心就对了,例如sum 是5,S是2的话其实就是无解的,所以:
if ((S + sum) % 2 == 1) return 0; // 此时没有方案同时如果 S的绝对值已经大于sum,那么也是没有方案的。
if (abs(S) > sum) return 0; // 此时没有方案再回归到01背包问题,为什么是01背包呢?
因为每个物品(题目中的1)只用一次!
这次和之前遇到的背包问题不一样了,之前都是求容量为j的背包,最多能装多少。
本题则是装满有几种方法。其实这就是一个组合问题了。
- 确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[i]种方法
其实也可以使用二维dp数组来求解本题,dp[i][j]:使用 下标为[0, i]的nums[i]能够凑满j(包括j)这么大容量的包,有dp[i][j]种方法。
下面我都是统一使用一维数组进行讲解, 二维降为一维(滚动数组),其实就是上一层拷贝下来,这个我在动态规划:关于01背包问题,你该了解这些!(滚动数组)也有介绍。
- 确定递推公式
有哪些来源可以推出dp[j]呢?
不考虑nums[i]的情况下,填满容量为j - nums[i]的背包,有dp[j - nums[i]]种方法。
那么只要搞到nums[i]的话,凑成dp[j]就有dp[j - nums[i]] 种方法。
举一个例子,nums[i] = 2: dp[3],填满背包容量为3的话,有dp[3]种方法。
那么只需要搞到一个2(nums[i]),有dp[3]方法可以凑齐容量为3的背包,相应的就有多少种方法可以凑齐容量为5的背包。
那么需要把 这些方法累加起来就可以了,dp[j] += dp[j - nums[i]]
所以求组合类问题的公式,都是类似这种:
dp[j] += dp[j - nums[i]]
这个公式在后面在讲解背包解决排列组合问题的时候还会用到!
- dp数组如何初始化
从递归公式可以看出,在初始化的时候dp[0] 一定要初始化为1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递归结果将都是0。
dp[0] = 1,理论上也很好解释,装满容量为0的背包,有1种方法,就是装0件物品。
dp[j]其他下标对应的数值应该初始化为0,从递归公式也可以看出,dp[j]要保证是0的初始值,才能正确的由dp[j - nums[i]]推导出来。
- 确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组)中,我们讲过对于01背包问题一维dp的遍历,nums放在外循环,target在内循环,且内循环倒序。
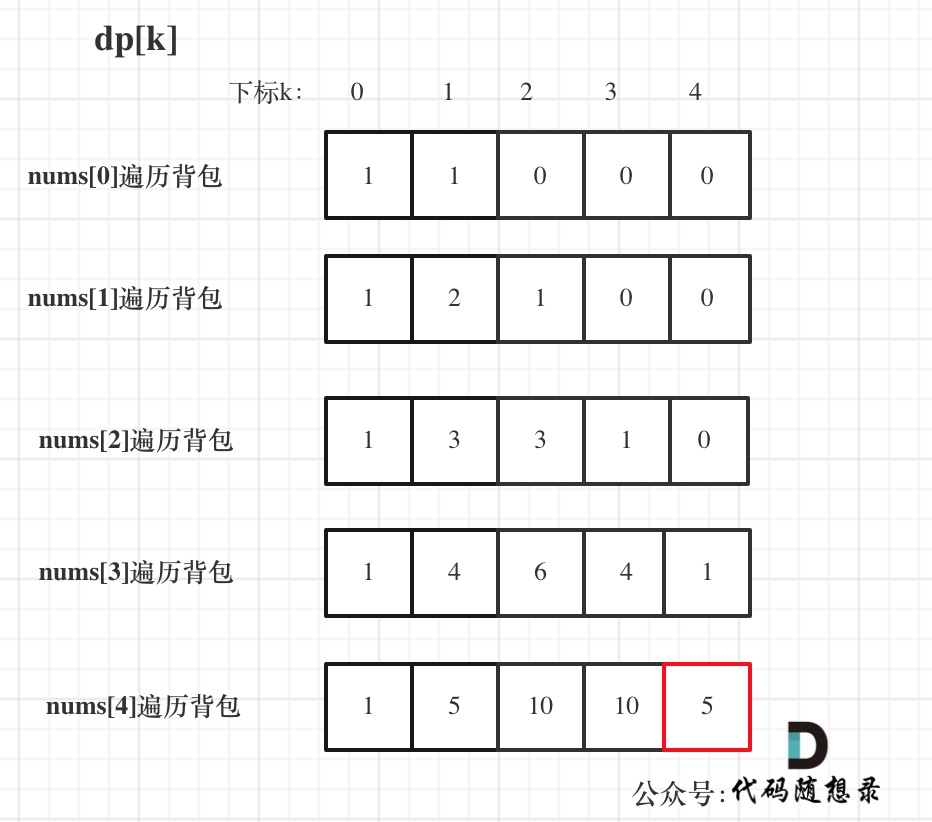
- 举例推导dp数组
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
C++代码如下:
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int S) {
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
if (abs(S) > sum) return 0; // 此时没有方案
if ((S + sum) % 2 == 1) return 0; // 此时没有方案
int bagSize = (S + sum) / 2;
vector<int> dp(bagSize + 1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); i++) {
for (int j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
}
};
- 时间复杂度O(n * m),n为正数个数,m为背包容量
- 空间复杂度:O(m) m为背包容量
此时 大家应该不仅想起,我们之前讲过的回溯算法:39. 组合总和是不是应该也可以用dp来做啊?
是的,如果仅仅是求个数的话,就可以用dp,但回溯算法:39. 组合总和要求的是把所有组合列出来,还是要使用回溯法爆搜的。
本题还是有点难度,大家也可以记住,在求装满背包有几种方法的情况下,递推公式一般为:
dp[j] += dp[j - nums[i]];
后面我们在讲解完全背包的时候,还会用到这个递推公式!
Java:
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum = 0;
for (int i = 0; i < nums.length; i++) sum += nums[i];
if ((target + sum) % 2 != 0) return 0;
int size = (target + sum) / 2;
if(size < 0) size = -size;
int[] dp = new int[size + 1];
dp[0] = 1;
for (int i = 0; i < nums.length; i++) {
for (int j = size; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[size];
}
}Python:
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
sumValue = sum(nums)
if target > sumValue or (sumValue + target) % 2 == 1: return 0
bagSize = (sumValue + target) // 2
dp = [0] * (bagSize + 1)
dp[0] = 1
for i in range(len(nums)):
for j in range(bagSize, nums[i] - 1, -1):
dp[j] += dp[j - nums[i]]
return dp[bagSize]Go:
func findTargetSumWays(nums []int, target int) int {
sum := 0
for _, v := range nums {
sum += v
}
if target > sum {
return 0
}
if (sum+target)%2 == 1 {
return 0
}
// 计算背包大小
bag := (sum + target) / 2
// 定义dp数组
dp := make([]int, bag+1)
// 初始化
dp[0] = 1
// 遍历顺序
for i := 0; i < len(nums); i++ {
for j := bag; j >= nums[i]; j-- {
//推导公式
dp[j] += dp[j-nums[i]]
//fmt.Println(dp)
}
}
return dp[bag]
}Javascript:
const findTargetSumWays = (nums, target) => {
const sum = nums.reduce((a, b) => a+b);
if(target > sum) {
return 0;
}
if((target + sum) % 2) {
return 0;
}
const halfSum = (target + sum) / 2;
nums.sort((a, b) => a - b);
let dp = new Array(halfSum+1).fill(0);
dp[0] = 1;
for(let i = 0; i < nums.length; i++) {
for(let j = halfSum; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[halfSum];
};