Skip to content

Latest commit

 

History

History
120 lines (107 loc) · 10.1 KB

数据结构与算法——二叉平衡树(AVL树)详解.md

File metadata and controls

120 lines (107 loc) · 10.1 KB
Raw

@TOC

AVL树概念

前面学习二叉查找树和二叉树的各种遍历，但是其查找效率不稳定(斜树)，而二叉平衡树的用途更多。查找相比稳定很多。(欢迎关注数据结构专栏)

  • AVL树是带有平衡条件的二叉查找树。这个平衡条件必须要容易保持。而且要保证它的深度是O(logN).
  • AVL的条件是左右树的高度差（平衡因子）不大于1；并且它的每个子树也都是平衡二叉树。
  • 对于平衡二叉树的最小个数，n0=0;n1=1;nk=n(k-1)+n(k-2)+1;(求法可以类比斐波那契！)

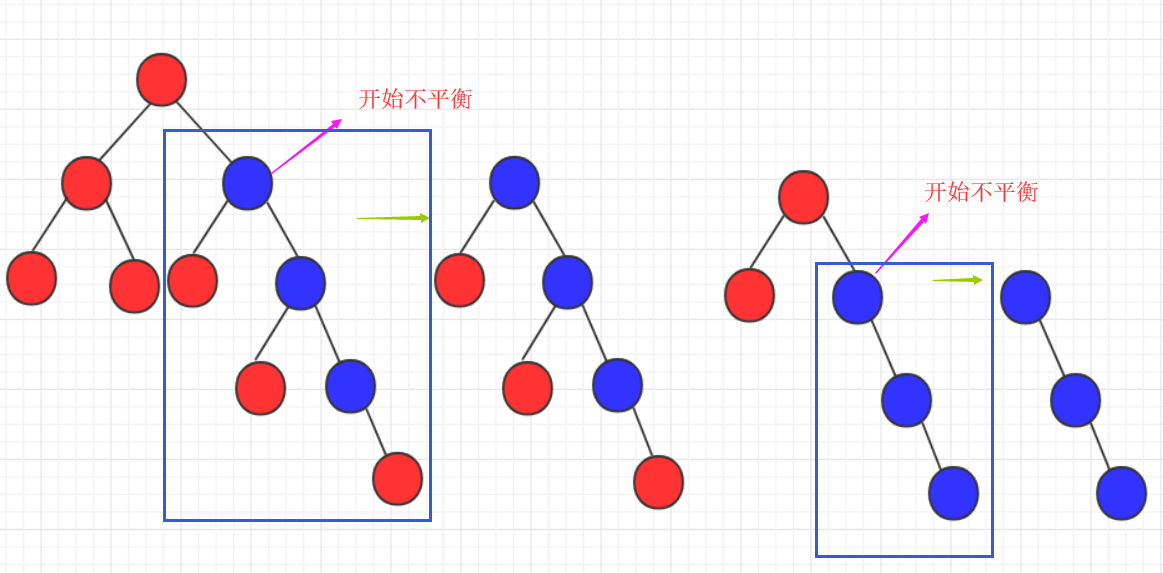
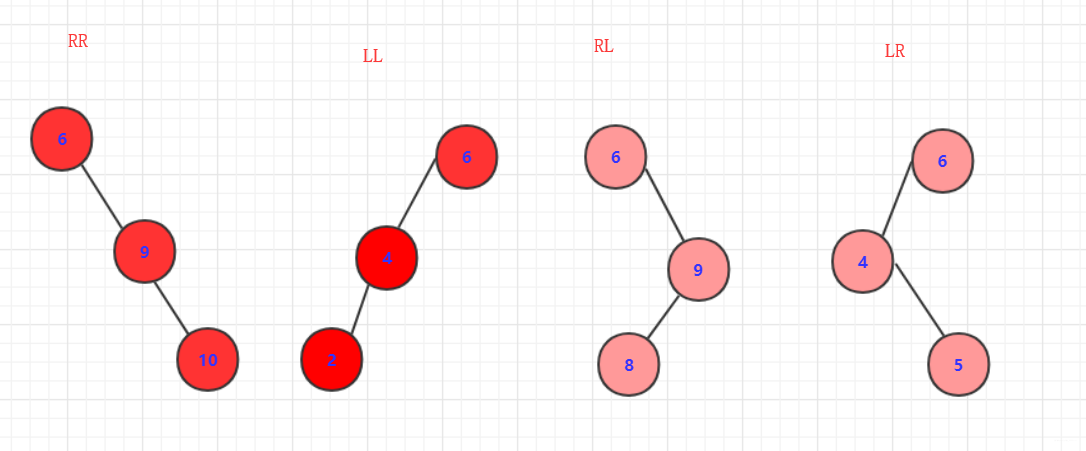
难点：AVL是一颗二叉排序树，用什么样的规则或者规律让它能够在复杂度不太高的情况下实现动态平衡呢？ 在这里插入图片描述

不平衡概况

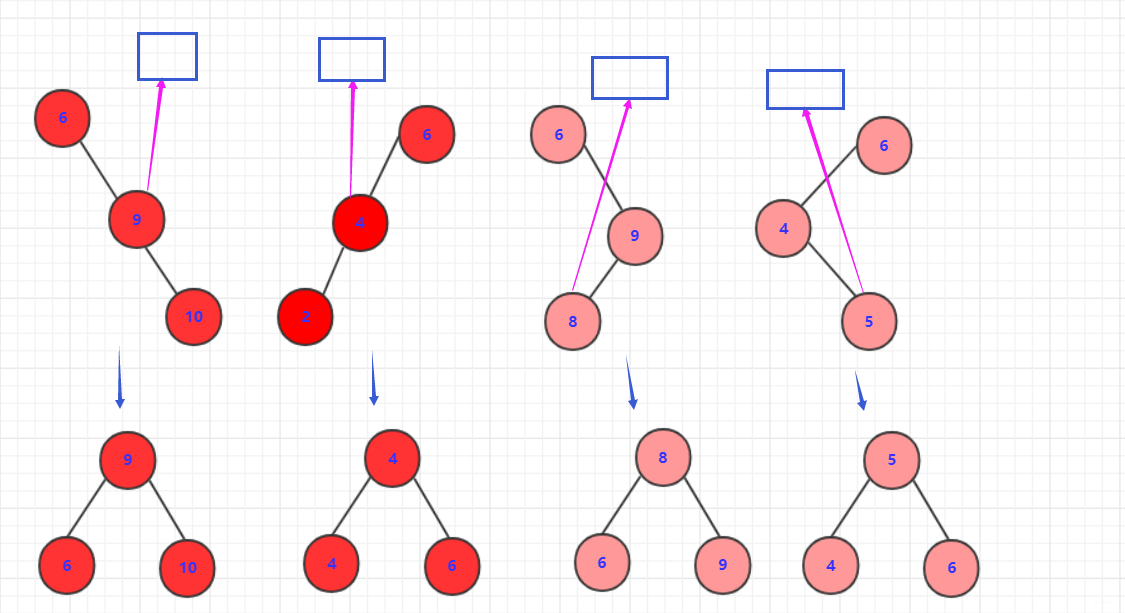
在这里插入图片描述 如果简单的以单节点看，大致有上面四种情形，并且他们的最后结果也是有的有所相近。只是：上下会变动。该在左面的还在左面，改在右面的还在右面。 在这里插入图片描述 这只是针对在底部，对于可能出现的平衡要首先搞清楚： 在这里插入图片描述 所以针对四种不平衡，可能出现在底部，也可能出现在头，也可能出现在某个中间节点导致不平衡。 而我们只需要研究其首次不平衡点，解决之后整棵树即继续平衡。当然，在实际解决肯定会带上递归的思想解决问题。

四种平衡旋转方式

RR平衡旋转(左单旋转)

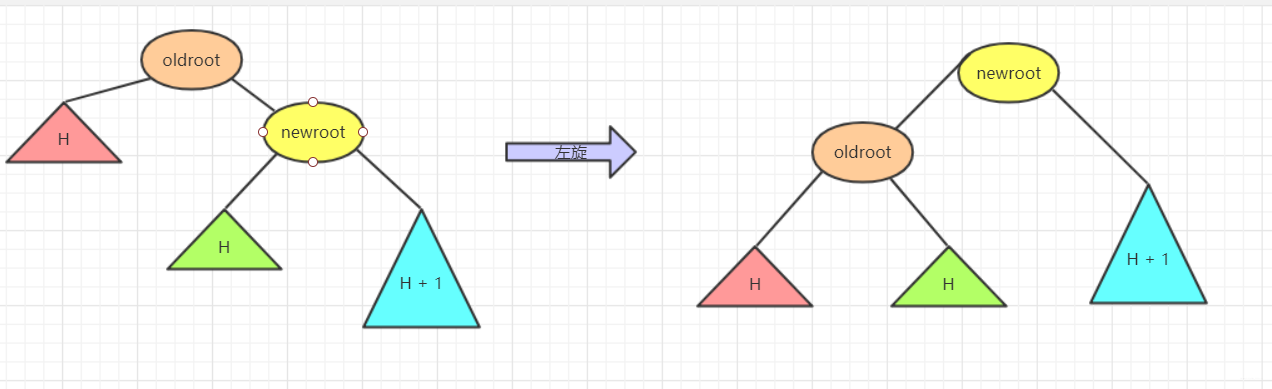
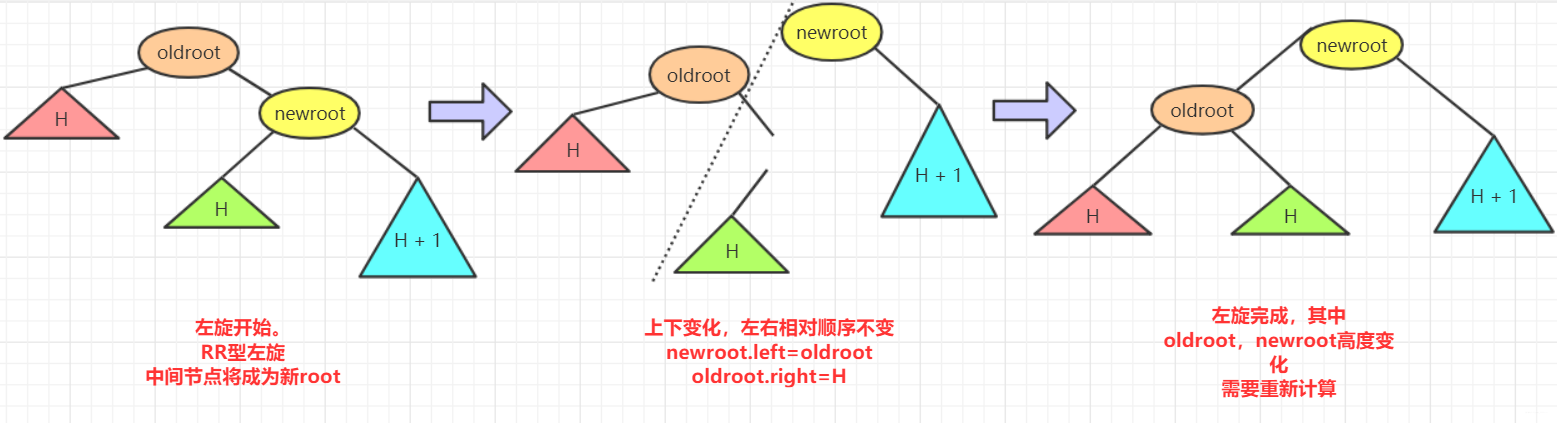
在这里插入图片描述 出现这种情况的原因是节点的右侧的右侧较深这时候不平衡节点需要左旋。再细看过程。

  • 再左旋的过程中，root(oldroot)节点下沉，中间节点(newroot)上浮.而其中中间节点(newroot)的右侧依然不变。
  • 它上浮左侧所以需要指向根节点(oldroot)(毕竟一棵树)。但是这样newroot原来左侧节点H空缺。而我们需要仍然让整个树完整并且满足二叉排序树的规则。
  • 而刚好本来oldroot右侧指向newroot变成oldroot被newroot左侧指向。所以oldroot右侧空缺，刚好这个位置满足在oldroot的右侧。在newroot的左侧。.所以我们将H插入在这个位置。
  • 其中H可能为NULL。不过不影响操作！ 在这里插入图片描述 而左旋的代码可以表示为：
private node getRRbanlance(node oldroot) {//右右深，需要左旋
	// TODO Auto-generated method stub
	node newroot=oldroot.right;
	oldroot.right=newroot.left;
	newroot.left=oldroot;
	oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
	newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新计算
	return newroot;		
}

LL平衡旋转(右单旋转)

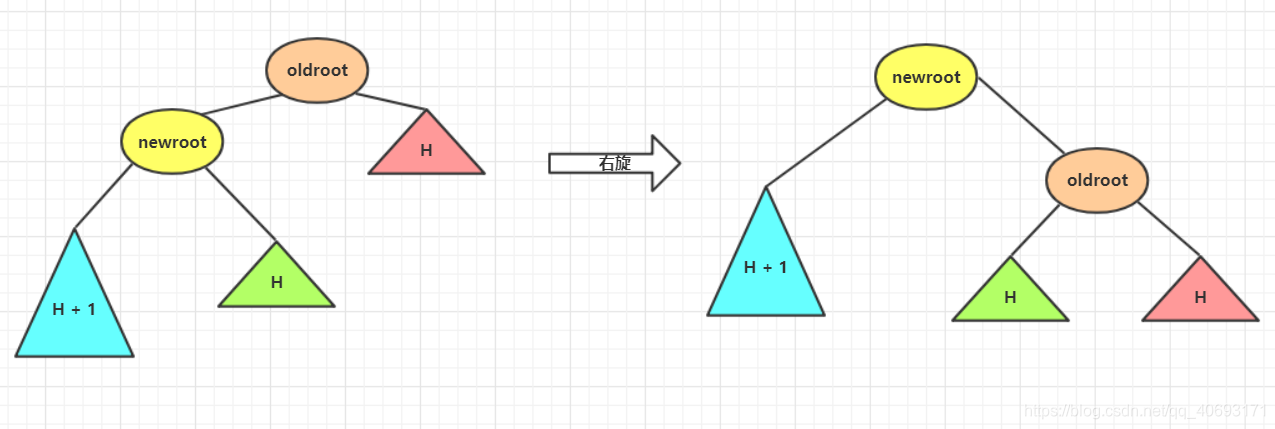
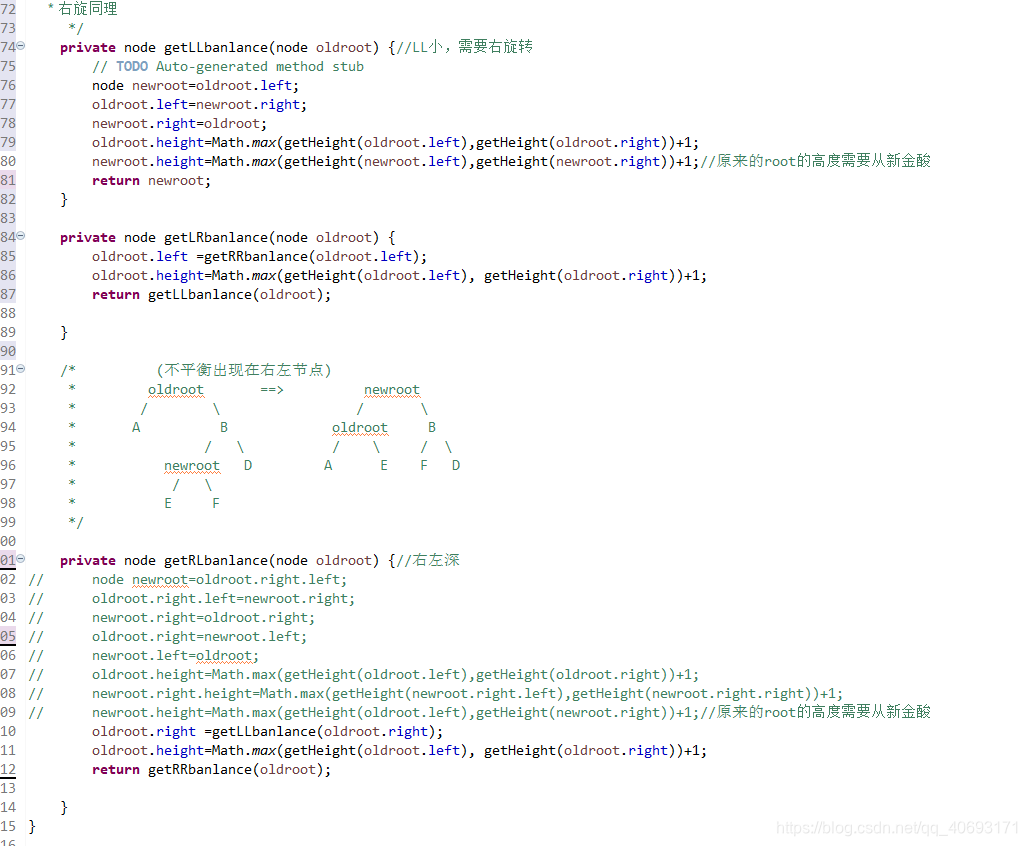
而右旋和左旋相反，但是思路相同，根据上述进行替换即可！ 在这里插入图片描述 代码：

private node getLLbanlance(node oldroot) {//LL小，需要右旋转
	// TODO Auto-generated method stub
	node newroot=oldroot.left;
	oldroot.left=newroot.right;
	newroot.right=oldroot;
	oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
	newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新金酸	
	return newroot;	
}

RL平衡旋转(先右后左双旋转)

产生不平衡的条件原因是：

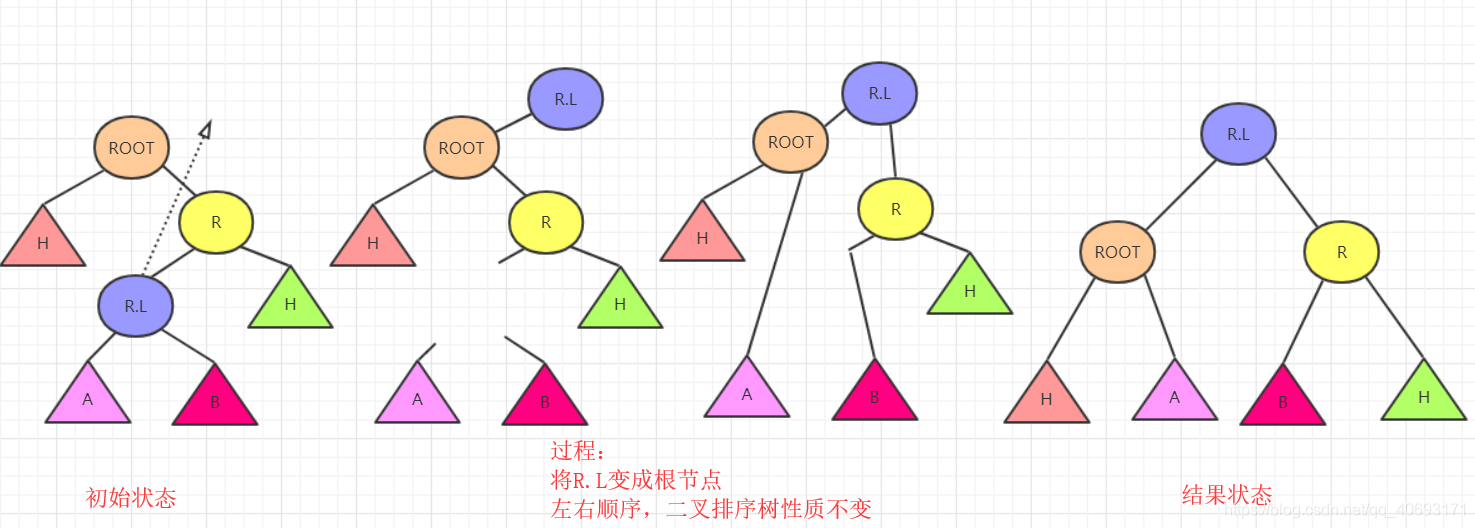
  • root节点右侧左侧节点的深度高些，使得与左侧的差大于1.这个与我们前面看到的左旋右旋不同的是因为它的结构不能直接变一下就可以完成。
  • 因为对于右左结构，中间的最大，两侧的最小。但是下面的比上面大(下面在上面右侧)所以如果平衡的话，那么右左的R.L应该在中间，而R应该在右侧。原来的root在左侧。
  • 所以节点的变化浮动比较大，而且需要妥善处理各个子节点的移动使其满足二叉排序树的性质！
  • 期间考虑树高度变化即可！

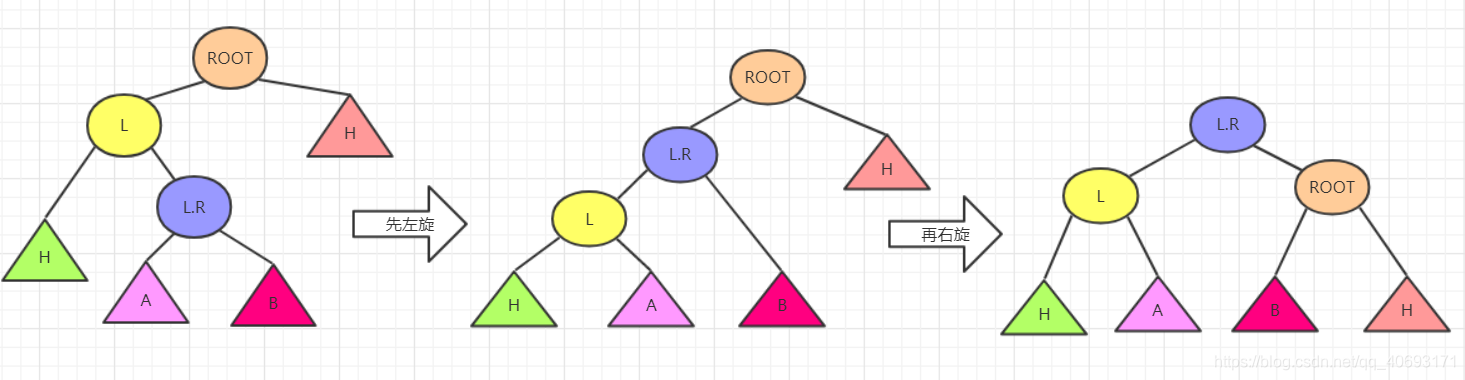
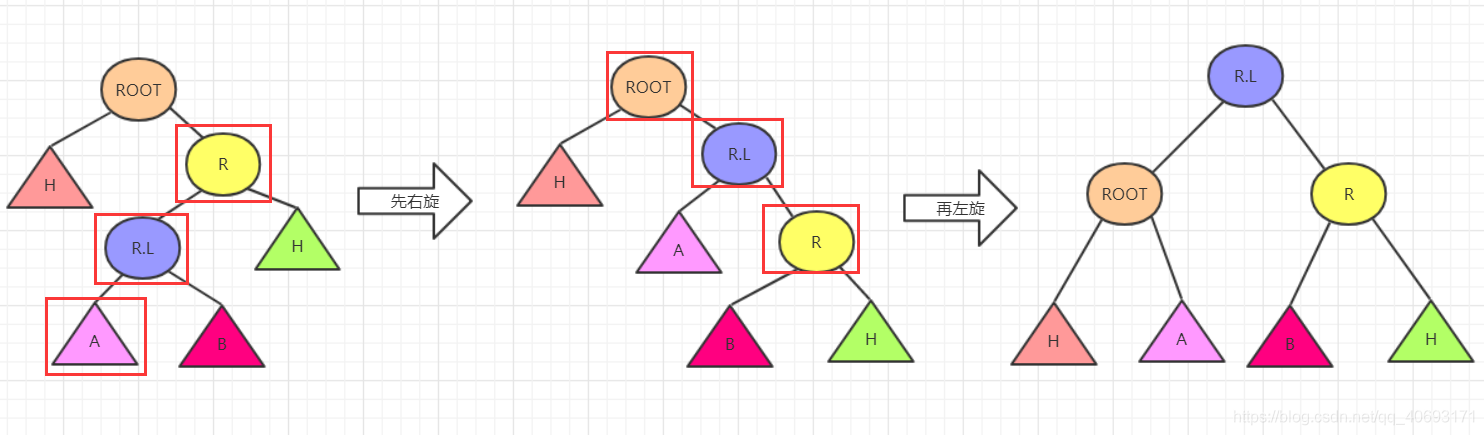
这种双旋转其实也很简单。不要被外表唬住。基于前面的单旋转，双旋转有两种具体逻辑思路。 思路1：两次旋转RR,LL 在这里插入图片描述 根据上图所圈的，先对底部使得底部的大小关系变化，使其在满足二叉平衡树的条件下还满足RR结构的二叉树。所以只需要对右节点R先进行右旋,再对ROOT进行左旋即可。 思路2：直接分析 根据初始和结果的状态，然后分析各个节点变化顺序。手动操作这些节点即可！

  • 首先根据ROOT,R,R.L三个节点变化。R.L肯定要在最顶层。左右分别指向ROOT和R。那么这其中R.left，ROOT.right发生变化(原来分别是R,L和R)暂时为空。而刚好根据左右大小关系可以补上R.L的左右节点。
  • 这样思考整棵树也可以完成平衡，但是要考虑树的高度变化。 在这里插入图片描述 代码为：(注释部分为方案1)
private node getRLbanlance(node oldroot) {//右左深	
//		node newroot=oldroot.right.left;
//		oldroot.right.left=newroot.right;
//		newroot.right=oldroot.right;
//		oldroot.right=newroot.left;	
//		newroot.left=oldroot;
//		oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;
//		newroot.right.height=Math.max(getHeight(newroot.right.left),getHeight(newroot.right.right))+1;
//		newroot.height=Math.max(getHeight(oldroot.left),getHeight(newroot.right))+1;//原来的root的高度需要从新金酸	
	oldroot.right =getLLbanlance(oldroot.right);
	oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1;
	return getRRbanlance(oldroot);
		
	}

LR平衡旋转(先左后右单旋转)

根据上述RL修改即可 在这里插入图片描述

private node getLRbanlance(node oldroot) {
	oldroot.left =getRRbanlance(oldroot.left);
	oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1;
	return getLLbanlance(oldroot);
		
	}

java代码实现

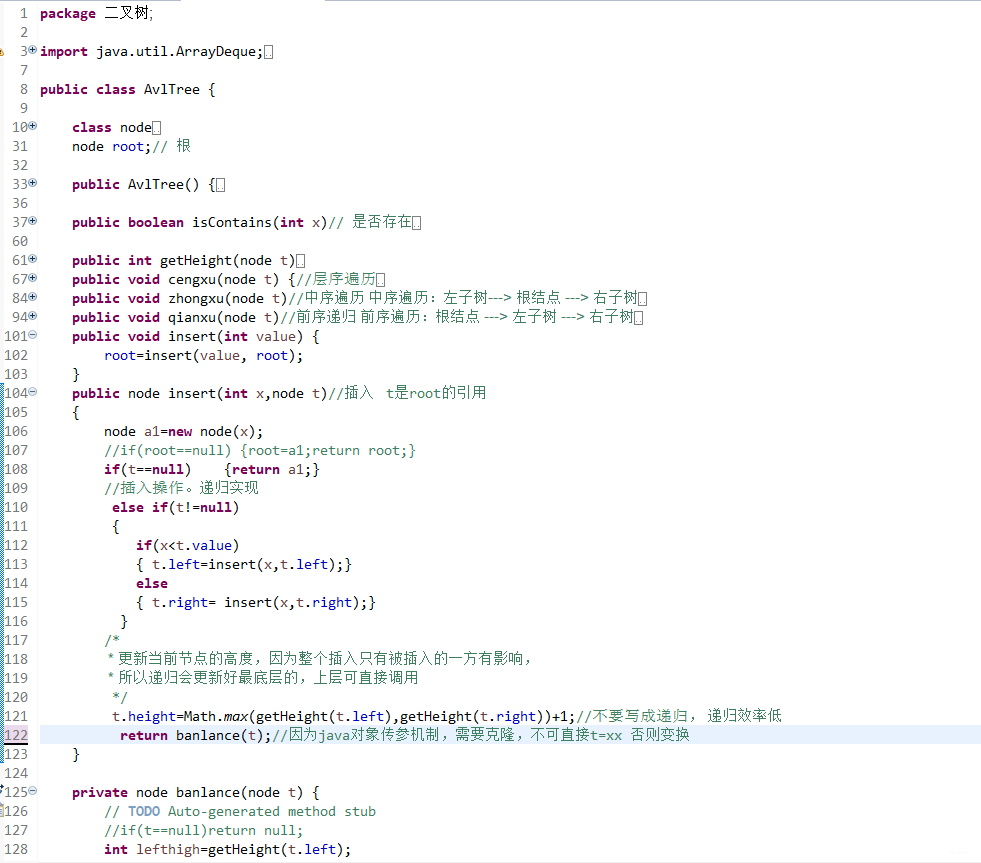
  • 首先对于节点多个height属性。用于计算高度(平衡因子)
  • 插入是递归插入。递归一个来回的过程，去的过程进行插入。**回的过程进行高度更新。和检查是否平衡。**不要写全局递归计算高度，效率太低下。事实上高度变化只和插入和平衡有关，仔细考虑即不会有疏漏！ 在这里插入图片描述 在这里插入图片描述 在这里插入图片描述

总结

测试情况： 在这里插入图片描述

  • AVL的理解需要时间，当然笔者的AVL自己写的可能有些疏漏，如果有问题还请各位一起探讨！
  • 当然，除了插入，AVL还有删除等其他操作，(原理相似。删除后平衡)有兴趣可以一起研究。
  • 如果需要源码还请关注笔者公众号：公众号查看相关专题文章！
  • 如果对后端、爬虫、数据结构算法等感性趣欢迎关注我的个人公众号交流：bigsai(回复数据结构、爬虫、java等有精心准备资料一份！)