LeetCode 62不同路径.md

LeetCode 62不同路径

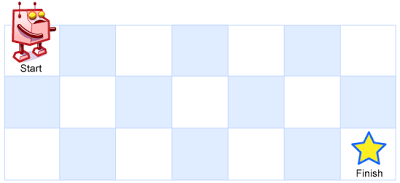
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

示例 1:

输入: m = 3, n = 2 输出: 3 解释: 从左上角开始，总共有 3 条路径可以到达右下角。 1 . 向右 -> 向右 -> 向下 2 . 向右 -> 向下 -> 向右 3 . 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3 输出: 28

提示：

1 <= m, n <= 100 题目数据保证答案小于等于 2 * 10 ^ 9

分析：

可用搜素，但是更是入门级别的动态规划。其状态方程为： 在dp[i][j]=dp[i-1][j]+dp[i][j-1];当然有特殊情况是需要考虑的，就是最上一行和最左一列以及起始位置。因为会出现越界的情况。

• 你可以特殊判断，先处理边界然后再进行计算。
• 但是你也可以像我一样，设置的二维数组扩大一点，把边界也当成一个普通情况处理，只不过将dp[0][1]或者dp[1][0]其中设为一个能够正确计算dp[1][1]=1即可(妙啊)。

实现代码为：

public int uniquePaths(int m, int n) {
    int dp[][]=new int[m+1][n+1];
    dp[0][1]=1;
    for(int i=1;i<m+1;i++)
    {
        for(int j=1;j<n+1;j++)
        {
            dp[i][j]=dp[i-1][j]+dp[i][j-1];
        }
    }
    return  dp[m][n];
}

结语

原创不易，bigsai请你帮两件事帮忙一下:

1. star支持一下， 您的肯定是我在平台创作的源源动力。

2. 微信搜索「bigsai」，关注我的公众号，不仅免费送你电子书，我还会第一时间在公众号分享知识技术。加我还可拉你进力扣打卡群一起打卡LeetCode。

记得关注、咱们下次再见！