Skip to content

Latest commit

 

History

History
186 lines (131 loc) · 7.54 KB

README.md

File metadata and controls

186 lines (131 loc) · 7.54 KB
Raw

Feynman Path Sum Diagram for Quantum Circuits

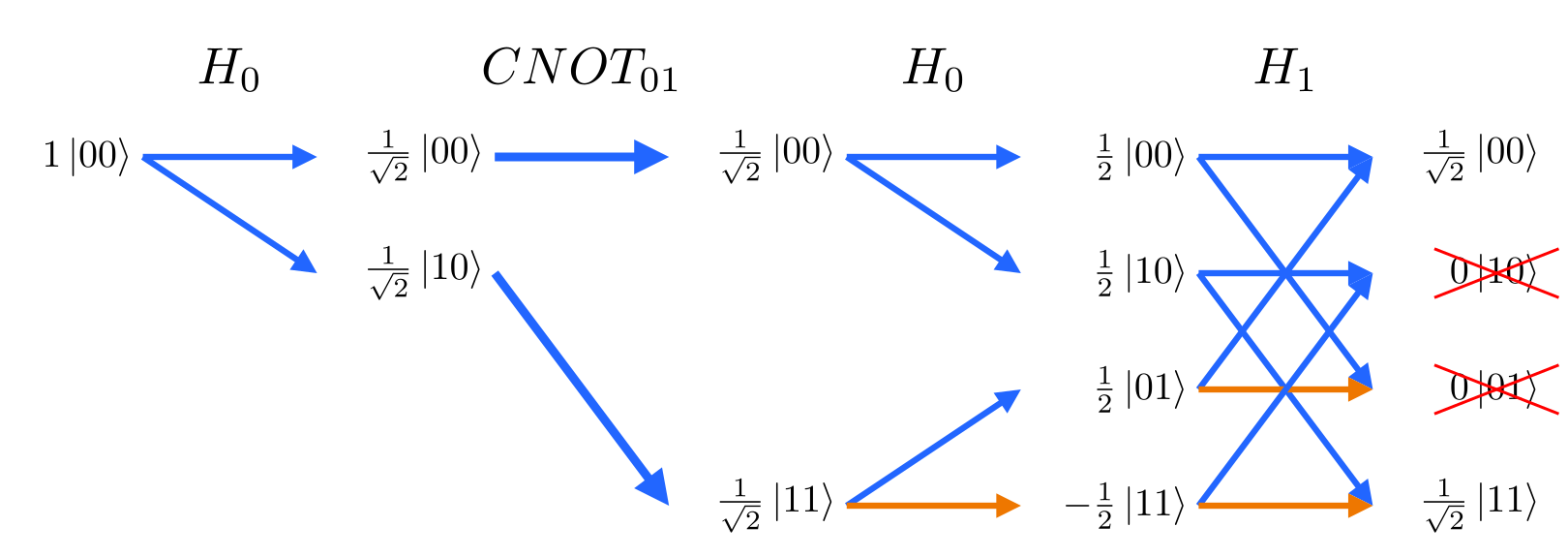
A visualization tool for the Feynman Path Sum applied to quantum circuits. The path integral formulation is an interpretation of quantum mechanics that can aid in understanding superposition and interference.

Path sum:

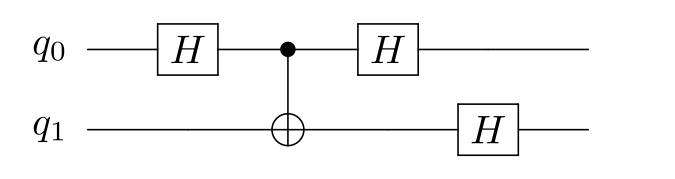
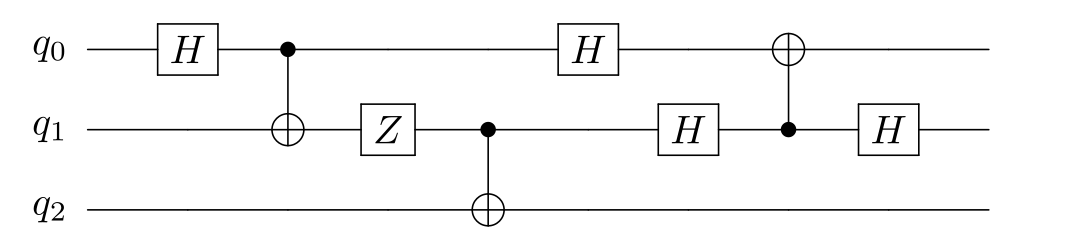
Circuit diagram:

How to read a path sum diagram:

  • Time flows from left to right as gates are executed on qubits.
  • Arrows transition from one state to another and traversing the arrows gives a path to an output.
  • Two diverging arrows indicate a split into two potential outcomes.
  • An orange arrow indicates a negative sign is added to that outcome.
  • When two arrows converge, the amplitudes are summed.
  • Quantum interference is when positive and negative amplitudes cancel in this sum.
  • The rightmost column lists the possible measurement outcomes along with the final probability amplitudes of measuring each outcome.

See also: Bloch sphere visualization

Install

feynman_path is available on PyPI:

python3 -m pip install feynman_path

Prerequisites

Several non-python tools are used to generate the graphics and various output formats. These non-python dependencies are listed below and platform-specific installation instructions can be found here.

  • LaTeX: A distribution of LaTeX that provides the pdflatex command needs to be installed separately. Used to generate the gate and state labels.
  • pdf2svg: Used to convert the LaTeX expressions into SVG elements.
  • Inkscape (optional): Only required to convert the output to PDF format.
  • Cairo (optional): Only required to convert the output to PNG format.

Ubuntu

sudo apt install texlive pdf2svg inkscape libcairo2  # Or texlive-latex-recommended, or texlive-latex-extra

macOS

Using homebrew:

brew install --cask mactex inkscape
brew install pdf2svg cairo

Usage

This package provides a command line tool to generate diagrams.

Examples

feynman_path interference 2 h0 cnot0,1 z1 h0 h1 cnot1,0 h1

feynman_path interference 2 h0 cnot0,1 z1 h0 h1 cnot1,0 h1 --circuit

Command line options

$ feynman_path -h
usage: feynman_path [-h] [--svg] [--png] [--pdf] [--sequence] [--circuit]
                    [--scale SCALE] [--verbose]
                    name n_qubits gate [gate ...]

Renders a Feynman path sum diagram for a sequence of quantum gates.

positional arguments:
  name           The file name to save (excluding file extension)
  n_qubits       The number of qubits in the quantum circuit
  gate           List of gates to apply (e.g. h0 z1 cnot0,1)

optional arguments:
  -h, --help     show this help message and exit
  --svg          Save diagram as an SVG image (default)
  --png          Save diagram as a PNG image
  --pdf          Save diagram as a PDF document
  --sequence     Save a sequence of images that build up the diagram from left
                 to right as <name>-nn.svg/png/pdf
  --circuit      Save a standard quantum circuit diagram named
                 <name>-circuit.svg/png/pdf instead of a Feynman path diagram
  --scale SCALE  Scales the resolution of the diagram when saved as a PNG
  --verbose      Print extra progress information

Python Package

feynman_path also provides a Python 3 package as an alternative to the command line tool. Diagrams can be viewed directly in a Jupyter notebook or saved.

import feynman_path

n_qubits = 3
font = 12
ws_label = 4+0.55*n_qubits  # Label width relative to font size
w_time = 60+ws_label*font  # Diagram column width
f = feynman_path.Diagram(
    n_qubits, font=font, ws_label=ws_label, w_time=w_time)

f.perform_h(0)
f.perform_cnot(0, 1)
f.perform_z(1)
f.perform_cnot(1, 2, pre_latex=r'\color{red!80!black}')
f.perform_h(0)
f.perform_h(1)
f.perform_cnot(1, 0)

f.draw()  # Display in Jupyter
f.draw().save_svg('output.svg')  # Save SVG
f.draw().set_pixel_scale(2).save_png('output.png')  # Save PNG
import latextools
latextools.svg_to_pdf(f.draw()).save('output.pdf')  # Save PDF

See examples/render_examples.py for more example code.

Examples

Using the CNOT gate to entangle qubits

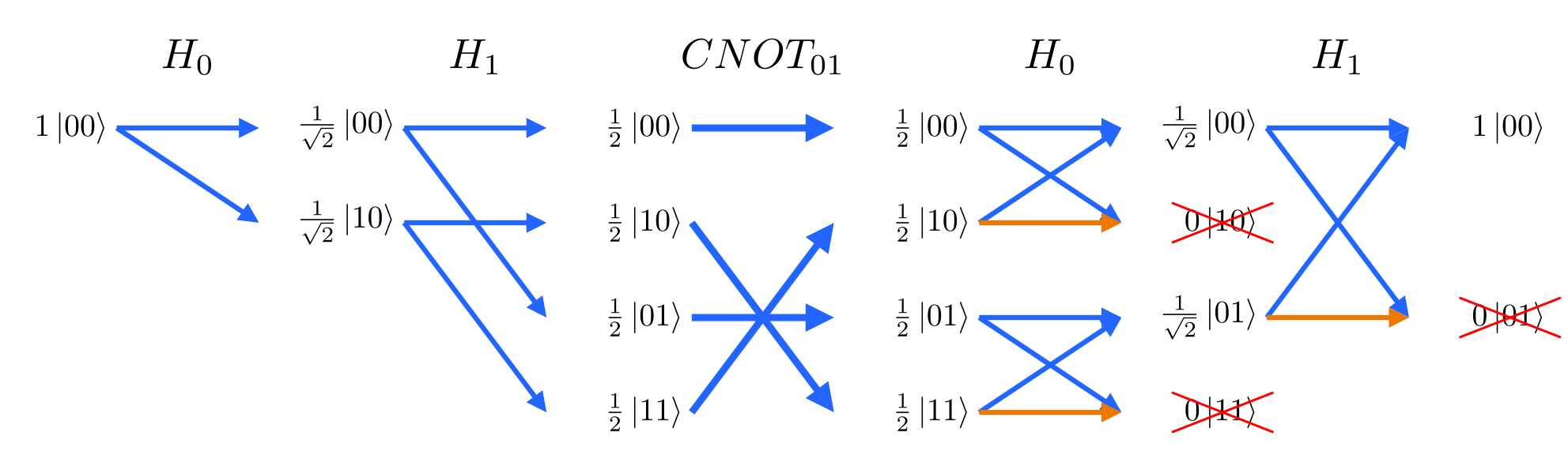
The CNOT gate (⋅–⨁) can be used to entangle two qubits, creating a Bell pair, but for certain input qubit states, the CNOT will have no effect.

Create a Bell pair by using a CNOT on the |+0⟩ state (q0=|+⟩, q1=|0⟩):

Note the output (rightmost) column is an entangled state: |00⟩+|11⟩

feynman_path no-entanglement 2 h0 cnot0,1 h0 h1

Fail to create a bell pair by using a CNOT on the |++⟩ state (q0=|+⟩, q1=|+⟩):

feynman_path no-entanglement 2 h0 h1 cnot0,1 h0 h1

Note the output (rightmost) column is a separable state: |00⟩

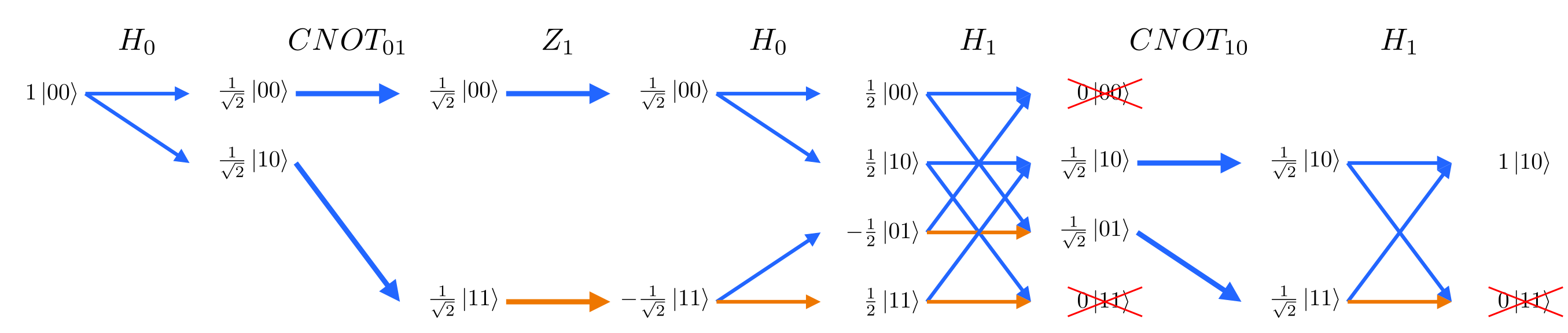
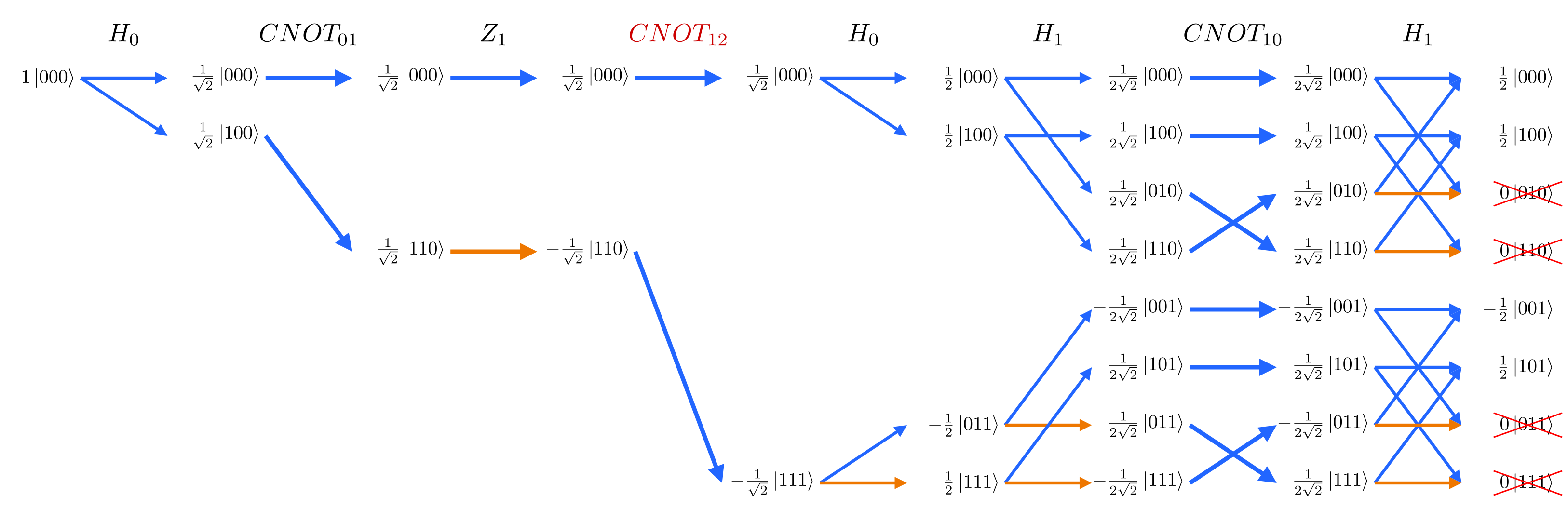
Copying an intermediate qubit state onto an ancilla ruins interference

In classical computing, it is common to inspect intermediate steps of a computation. This can be very useful for debugging. In quantum computing however, this destroys the effect of interference. We can use a CNOT gate (⋅–⨁) to copy an intermediate value onto another qubit to inspect later. Shown below, copying the intermediate value of q1 to q2 changes the output of q0, q1.

Original circuit that compute the output q0=1, q1=0:

feynman_path interference 2 h0 cnot0,1 z1 h0 h1 cnot1,0 h1

The addition of CNOT1,2 to inspect the intermediate value of q1 changes the output of q0:

Note how the path diagram is the same except the arrows at H1 are now split into the upper and lower halves of the diagram and don't interfere anymore.

feynman_path no-interference 3 h0 cnot0,1 z1 cnot1,2 h0 h1 cnot1,0 h1