Problema del Flujo Máximo:
Dado un grafo que represente una red de flujo donde cada arista representa una capacidad, y teniendo además un nodo inicial ‘S’ y un nodo final ‘T’; encontrar el máximo flujo posible desde S hasta T.
Se tienen las siguientes limitantes:
- El flujo en una arista no debe superar su máxima capacidad
- El flujo que entra debe ser exactamente igual al flujo que sale para cada nodo, exceptuando S y T.
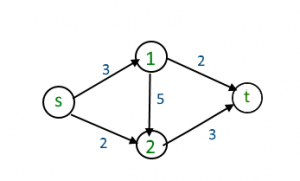
Ejemplo:
En el grafo de arriba podemos observar que se puede enviar un flujo de 3 de S a 1, luego llevar 2 de 1 a T, mientras que el flujo restante va de 1 a 2 y de 2 a T. Finalmente mandamos un flujo de 2 de S a 2 y de 2 a T, haciendo llegar un total de 5 a T, entonces este es nuestro máximo flujo.
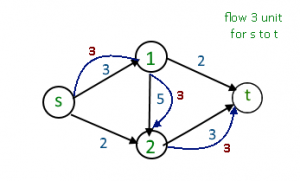
Existen muchos enfoques para resolver este problema, por ejemplo, un algoritmo ‘ingenuo’ intentaría tomar el camino de máximo flujo en cada nodo, sin embargo, esto no siempre nos lleva a la solución. Esto se puede observar si seguimos este algoritmo con el mismo grafo:
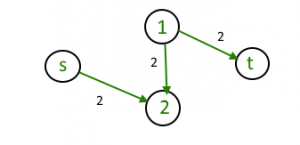
Este camino sumaría un flujo de 3 y dejaría el siguiente grafo:
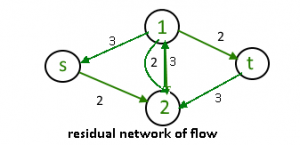
Pero ahora ya no hay forma de llevar más flujo. Para solucionar este problema, se utiliza un ‘grafo residual’, donde el flujo utilizado pasa a convertirse en un camino de regreso en lugar de desaparecer, de esta forma se puede ‘deshacer’ una acción y probar otros caminos.
Este concepto se aplica en el algoritmo de Ford-Fulkerson y en el de Dinic.