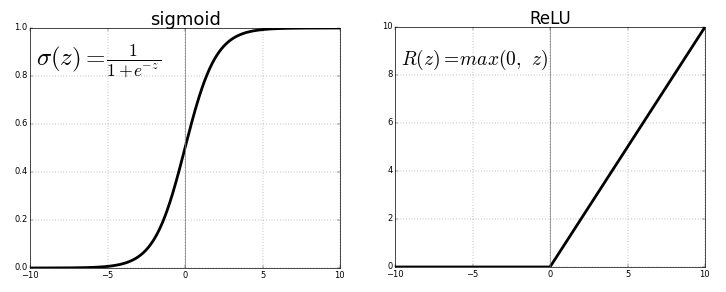(Matrix) Multi Layer Perceptron library for ESP32

New version of MLP, using matrix maths

Dependencies

• Uses my matrix linear algebra library (https://github.com/lesept777/Matrix-maths-for-ESP32-and-AI)
• The library LittleFS is used for loading / saving files on SPIFFS.
• You may also need to install the ESP32 data upload tool in the Arduino IDE. The LittleFS version is here. Some help to install it (in French) is here.

News

2022/05/18: The dataset is now created using Matrices, which accelerates the computations. More than 2x faster!

2022/08/01: Important change. To prepare the quantification of neural networks (i.e. using weights stored as int8_t instead of float), I rewrote the matrix linear algebra library. It is called now MatrixUT and must be imported with: #include "MatrixUT.hpp" in the sketch.

Description

This library is designed to be used with the Arduino IDE.

Multilayer perceptron is decribed here. This library implements both training and inference phases on a dataset. Datasets can be created in the sketch or read from a csv file. This library is not intended to work with images, only with arrays of floats.

It can address deep networks, made of one input layer, multiple hidden layers and one output layer. The output layer can have one neuron for regression, or several neurons for classification (use SIGMOID or SOFTMAX activation for the last layer).

Main features

• Uses matrix algebra (floating points 32 bits)
• Many activations available
• Can create dataset from csv file or from std::vector or arrays
• The user can split the dataset
• Single instruction optimization of the training phase, with options
  • The user can also build her/his own training code
• Many training options available:
  • Begin training on small dataset for faster training (don't use this with transfer learning)
  • Linear or logarithmic variation of the learning rate during the training phase
  • Quadratic variation of momentum during the training phase
  • Momentum and sigmoid gain can change if the cost does not decrease
  • Weights can be randomly alterred if the cost does not decrease
  • Gradient clipping, gradient scaling for faster convergence
  • Weights clipping to zero for sparsity
  • Network pruning for lower memory size
  • L1, L2 regularization available
  • Xavier initialization for weights
  • Displays training cost and validation cost, to watch for overfitting
• Verbose level can be set to have more or less convergence information
• Displays network and performance information at the end:
  • Confusion matrix
  • Layers informations
  • Weights statistics
• Can save the network's data on file for future usage (transfer learning)
• etc.

Multilayer perceptron

Multilayer perceptron is decribed here. This library implements both training and inference phases on a dataset. Datasets can be created in the sketch or read from a csv file. This library is not intended to work with images, only with arrays of floats.

Quick start

If you want to test it quickly, try the "sinus" example

Guidelines

First load the libraries:

#include <Matrix.h>
#include "MMLP.h"

Declare a network

To declare a network, just create an array of int with the number of neurons in each layer. The arguments of the constructor are: array of neurons, number of layers, verbose level.

// Declare the network
int Neurons[] = {2, 20, 1}; // Number of neurons in each layer (from input to output)
MLP Net(Neurons, 3, 1);     // Array of neurons, number of layers, verbose level

Declare the activations of each layer and set the hyperparameters.

int Activations[] = {RELU, RELU, SIGMOID};
Net.setActivations (Activations);
Net.setHyper(0.25f, 0.5f); // LR & momentum

Activation functions currently available:

• SIGMOID: S-shaped curve, between 0 and 1
• SIGMOID2: Similar to SIGMOID, but between -1 and +1
• TANH: Quite similar to SIGMOID2
• RELU: Rectified Linear Unit
• LEAKYRELU and ELU variants
• SELU : Scaled Exponential Linear Unit (prevents vanishing & exploding gradient problems)
• IDENTITY
• SOFTMAX

The sigmoid and hyperbolic tangent activation functions cannot be used in networks with many layers due to the vanishing gradient problem. In the backpropagation process, gradients tend to get smaller and smaller as we move backwards: neurons in earlier layers learn slower than neurons in the last layers. This leads to longer learning and less accurate prediction. The rectified linear activation function overcomes this problem, allowing models to learn faster and perform better.

Softmax for classification problems implemented. SOFTMAX can only be used for the last layer. If you choose it, the cost function is Cross entropy. Otherwise, it's Squared error.

Create a dataset

There are several ways to create a dataset:

• read data from a csv file (see Boston Housing example)
• create the data using a function:
  • declare the dataset from vectors of float
  • declare the dataset from arrays of float

The data can be normalized (several options available) using the normalizeDataset method. Then the dataset can be split in 3 parts: training data, validation data and test data. Use setTrainTestmethod:

Net.setTrainTest(0.7, 0.2, 0.1); // 70% training, 20% validation, 10% test
Net.setTrainTest(4, 1, 1);       // 4/6 = 66.66% training, 1/6 = 16.66% validation and test
Net.setTrainTest(0.8, 0., 0.2);  // 70% training, 0% validation, 20% test

normalizeDataset is used as follows:

Net.normalizeDataset(X, Y, opt);

opt ranges from 0 to 3:

• 0: no normalization
• 1: data normalzed in [0, 1]
• 2: data normalized in [-1, 1]
• 3: data normalized with 0 mean and 1 standar dev.