Feature Request: Binomial Coefficient Entropy Coding for Inverted Index Postings #334
Replies: 2 comments 1 reply
-
|
Hey @MurageKibicho ! If I understand your proposal correctly, you propose to change the encoding of the set of documents in the inverted index, so that the set of document ids is represented in the compact format you propose? Right now, the document ids set are represented in the RoaringBitmap format. The key advantage of this format is that, on top of provding decent compression, allows for extremely fast set operation enabled by SIMD. A key component to changing this encoding would be to have similar time and memory complexity on the set operations as Roaring does. What can you tell us about that? |
Beta Was this translation helpful? Give feedback.
-
|
Hey @MurageKibicho! If I understand correctly your proposal you are developing something similar to Daniel Lemire's SIMDComp library? Which has a Rust port by Paul Masurel. It uses similar principles than the one you showed by using the least amount of bits to represent runs of integers and combines that with SIMD instruction to keep a fast decoding throughput. As @MarinPostma says we already use the RoaringBitmap format to represent our inverted index integers, as it is easier to work with, it compiles everywhere (even in WASM) and it implements fast set operations already. Thank you anyway for your proposition it is very kind of you and maybe you can tell us more about the difference with the two libraries I talked about above. |
Beta Was this translation helpful? Give feedback.
-
Summary
This is a proposal for encoding inverted index integer sequences using a number system based on binomial coefficients.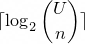
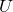 is largest number in the list and
is largest number in the list and 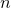 is the number of elements in the list.
is the number of elements in the list.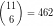 and
and
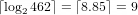 .
.
This number system is chosen because the minimum number of bits needed to encode a list of strictly increasing integers
is given by the equation
where
For example to encode the sequence 1,2,3,4,10,11 we need at least 9 bits:
Binary interpolative coding, one of the best methods for inverted list compression takes at least 20 bits to represent the example sequence. You can confirm this here.
However, if we represent the same sequence as a sum of binomial coefficients, it takes 10 bits to encode the list, and an extra 3 bits to store the length of the list. The total is 13 bits. You can confirm this here.
Motivation
Compression is a solved problem. The best compressors work by changing radixes, or number bases to find the most concise representation of data.
For instance, arithmetic coding is a generalized change of radix for coding
at the information theoretic entropy bound. This bound is a measure of redundancy - how many duplicates are in your data. Strictly increasing integer sequences have no duplicates, therefore, cannot be compressed
according to the information theoretic bound. This means huffman coding and arithmetic coding methods are inefficient with non-repetitive integer sequences.
This rfc proposes the use of the combinatorial number system to encode inverted index integer sequences at the combinatorial information theoretic entropy bound.
Just like arithmetic coding, this change in number systems allows us to encode integer sequences with the least number of bits.
I am a Math major in my junior year and if this RFC succeeds I would love to take a gap year and work on this library full time. The library
has sample code for converting between binary and the combinatorial number system using a greedy algorithm, or by generating a lookup table.
Technical design
Overview of Combinatorial Number System
Any natural number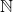 can be uniquely written as a sum of binomial coefficients
can be uniquely written as a sum of binomial coefficients
using this greedy algorithm.
Example: Find the combinatorial representation of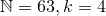
To reverse the process, sum your list of binomial coefficients
Comparison to Binary Interpolative Coding
In the example above, it can be seen that the sequence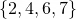
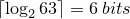 using the combinatorial number system with an extra 3 bits to store the length of the sequence. This is a total of 9 bits to encode this sequence.
using the combinatorial number system with an extra 3 bits to store the length of the sequence. This is a total of 9 bits to encode this sequence.
can be encoded in
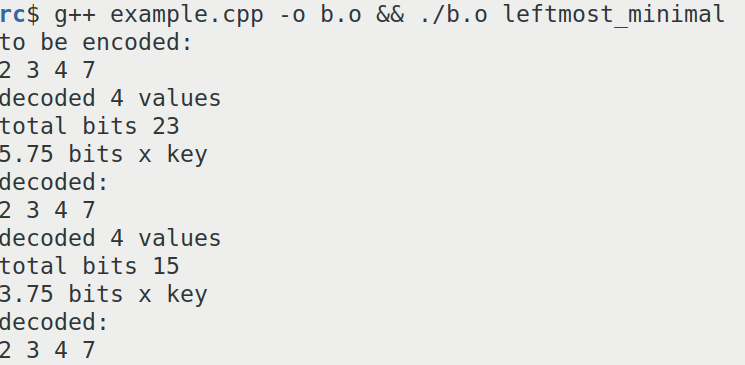
Using this library it can be confirmed that binary interpolative coding takes between 15 to 23 bits to encode the same sequence.
This is a screenshot of the result of binary interpolative coding.
The combinatorial number systems always encodes integer sequences at the entropy limit.
Beta Was this translation helpful? Give feedback.
All reactions