README_EN.md

106. Construct Binary Tree from Inorder and Postorder Traversal

中文文档

Description

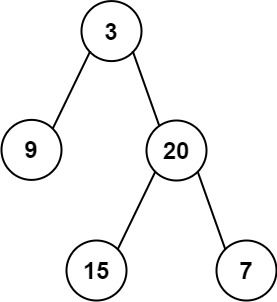
Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.

 

Example 1:

Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: inorder = [-1], postorder = [-1]
Output: [-1]

 

Constraints:

• 1 <= inorder.length <= 3000
• postorder.length == inorder.length
• -3000 <= inorder[i], postorder[i] <= 3000
• inorder and postorder consist of unique values.
• Each value of postorder also appears in inorder.
• inorder is guaranteed to be the inorder traversal of the tree.
• postorder is guaranteed to be the postorder traversal of the tree.

Solutions

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        if not postorder:
            return None
        v = postorder[-1]
        root = TreeNode(val=v)
        i = inorder.index(v)
        root.left = self.buildTree(inorder[: i], postorder[:i])
        root.right = self.buildTree(inorder[i + 1:], postorder[i:-1])
        return root

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private Map<Integer, Integer> indexes = new HashMap<>();

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        for (int i = 0; i < inorder.length; ++i) {
            indexes.put(inorder[i], i);
        }
        return dfs(inorder, postorder, 0, 0, inorder.length);
    }

    private TreeNode dfs(int[] inorder, int[] postorder, int i, int j, int n) {
        if (n <= 0) {
            return null;
        }
        int v = postorder[j + n - 1];
        int k = indexes.get(v);
        TreeNode root = new TreeNode(v);
        root.left = dfs(inorder, postorder, i, j, k - i);
        root.right = dfs(inorder, postorder, k + 1, j + k - i, n - k + i - 1);
        return root;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, int> indexes;

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        for (int i = 0; i < inorder.size(); ++i) indexes[inorder[i]] = i;
        return dfs(inorder, postorder, 0, 0, inorder.size());
    }

    TreeNode* dfs(vector<int>& inorder, vector<int>& postorder, int i, int j, int n) {
        if (n <= 0) return nullptr;
        int v = postorder[j + n - 1];
        int k = indexes[v];
        TreeNode* root = new TreeNode(v);
        root->left = dfs(inorder, postorder, i, j, k - i);
        root->right = dfs(inorder, postorder, k + 1, j + k - i, n - k + i - 1);
        return root;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(inorder []int, postorder []int) *TreeNode {
	indexes := make(map[int]int)
	for i, v := range inorder {
		indexes[v] = i
	}
	var dfs func(i, j, n int) *TreeNode
	dfs = func(i, j, n int) *TreeNode {
		if n <= 0 {
			return nil
		}
		v := postorder[j+n-1]
		k := indexes[v]
		root := &TreeNode{Val: v}
		root.Left = dfs(i, j, k-i)
		root.Right = dfs(k+1, j+k-i, n-k+i-1)
		return root
	}
	return dfs(0, 0, len(inorder))
}

...