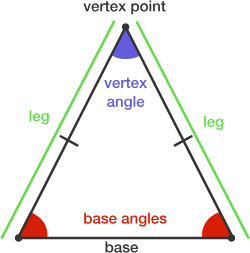
A simple library for identifying isosceles triangles within a set of 2d points.
I was working on building an interactive touchscreen table with object recognition features. This concept uses marker discs with a distinct isosceles triangle pattern to distinguish objects, therefore I needed a library to handle all the math for identifying and tracking these triangles.
You can find more information about this project here if you're interested.
- Identify distinct isosceles triangles within a given set of 2d points
- Match triangles to pre-defined vertex angles
- Calculate additional triangle properties like orientation, center, height etc.
Via NPM (recommended)
$ npm i --save tritraAlternatively you can simply copy dist/js/tritra.js to your project.
Include the package in your HTML page:
<script type="text/javascript" src="/path/to/tritra.js"></script>First create an instance of the triangle recognizer class tritra.Recognizer. This class does all the heavy lifting and you should only create it once during your application lifecycle. To create the recognizer you must supply an array of vertex angles which you'd like the recognizer class to look out for.
// we're looking for triangles with 18, 36 and 54 degrees vertex angles
var vertexAngles = [18, 36, 54];
// create the recognizer
var R = new tritra.Recognizer(vertexAngles);
Define a set of 2d points. The utility class tritra.Vector2d simply represents the X and Y coordinates of a 2d point.
var examplePoints = [
// defines a triangle with 36 degrees vertex angle
new tritra.Vector2d(300, 300),
new tritra.Vector2d(366, 300),
new tritra.Vector2d(333, 198)
];Finally try to identify the triangles within your set of points. You will receive an array with all matches as the result value:
var matches = R.findMatches(examplePoints);Each array item will be a tritra.Match object containing the details of the matching triangle:
var match = matches[0];
// index within your vertexAngles
console.log(match.index);
1
// the matched angle within the given tolerance (not the actual vertex angle)
console.log(match.matchedAngle);
36
// properties of the matched triangle
var centerPoint = match.getCenter();
console.log(centerPoint.x, centerPoint.y);
333, 266
// get the rotation (orientation) of the triangle in degrees
console.log(match.getOrientation());
-180More properties are available. Check the documentation of tritra.Match or have a look at the included example HTML file.
The main recognizer class which will identify triangles for you
An array of vertex angles of the isosceles triangles you want to identify. You must provide at least one vertex angle.
Currently supports two options:
maxPointDistance (default: 150): The maximum distance for two points to still be considered as part of the same triangle. You should adjust these according to your screen size and DPI.
As a general rule, the larger the screen and the higher the DPI, the higher you should set this value. Do not set it too high though as this will cause two nearby markers to no longer be recognized.
maxAngleTolerance (default: 5): The recognizer will consider vertex angles +- this value (in degrees) as still matching the nearest vertex angle. Do not set this value higher than half of the smallest distance between your configured vertex angles.
An array of tritra.Vector2d objects containing the points you want to analyze
Returns an array of tritra.Matches objects describing the identified triangles.
Simple wrapper object for a point in 2d space with x and y coordinates.
Represents a triangle defined by three points in 2d space. Points are expected as tritra.Vector2d objects.
Returns the clockwise orientation of the triangle in degrees as seen from its vertex angle. The vertex angle pointing south translates to zero degrees.
Returns the width of the triangle.
Returns the height of the triangle.
Returns the vertex angle (apex angle) of the triangle.
Returns a tritra.Vector2d coordinate representing the vertex point (apex point) of the triangle.
Returns a tritra.Vector2d coordinate representing the center point of the triangle.
Represents a match found by the recognizer based on a requested vertex angle. You will usually not create instances of this object by yourself but instead the recognizer will create it for you.
index: The index of the matched angle within your original vertexAngles parameter
matchedAngle: The matched angle. This is not the actual vertex angle but the configured vertex angle within the acceptable "maxAngleTolerance" (see above).
triangle: The raw matched tritra.Triangle object