Communication Topologies

In the theory of π-calculus, there is an important notion of static equivalence between terms: structural congruence ≡. Intuitively, if P ≡ Q then P and Q only differ by irrelevant syntactic details, such as the order of parallel components. By using structural congruence, one can always present a process in standard form:

  ν(x1,…,xn).(A1[…] | … | An[…])

In this form, every name is disambiguated, and all the parallel components are sequential processes Ai[…] (i.e. processes that are not parallel compositions themselves and are ready to execute an action). You can interpret a standard form as the runtime configuration of a system where each xi is an instance of a channel, and each thread Ai[y1,…,yn] is executing a program location Ai with local variables bound to channels [y1,…,yn].

Stargazer presents terms in graphical form. This graphics are a visualisation of what is called the communication topology of the system (aka network). The communication topology (topology for short) is obtained from a standard form by simply creating a node for each name and for each sequential process, and connecting the node of a name x and the one of a process A[y1,…,yn] if and only if some yi is x (i.e. if x occurs free in the process). Intuitively, there is an edge between a thread and each of the channels it currently knows (that is, the channels currently bound to its local variables).

For example:

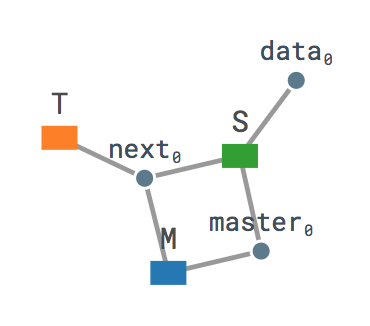
is the communication topology of the term

new next_0,data_0,master_0.( M[master_0,next_0] | S[next_0,master_0,data_0] | T[next_0] )

In Stargazer, thread nodes are represented by boxes and name nodes by dots. The colour of the box reflects the process identifier running in that node. Colours are automatically assigned to process identifiers, and you can inspect the mapping by selecting the "Legend" tab of the source code sidebar. For the example above: