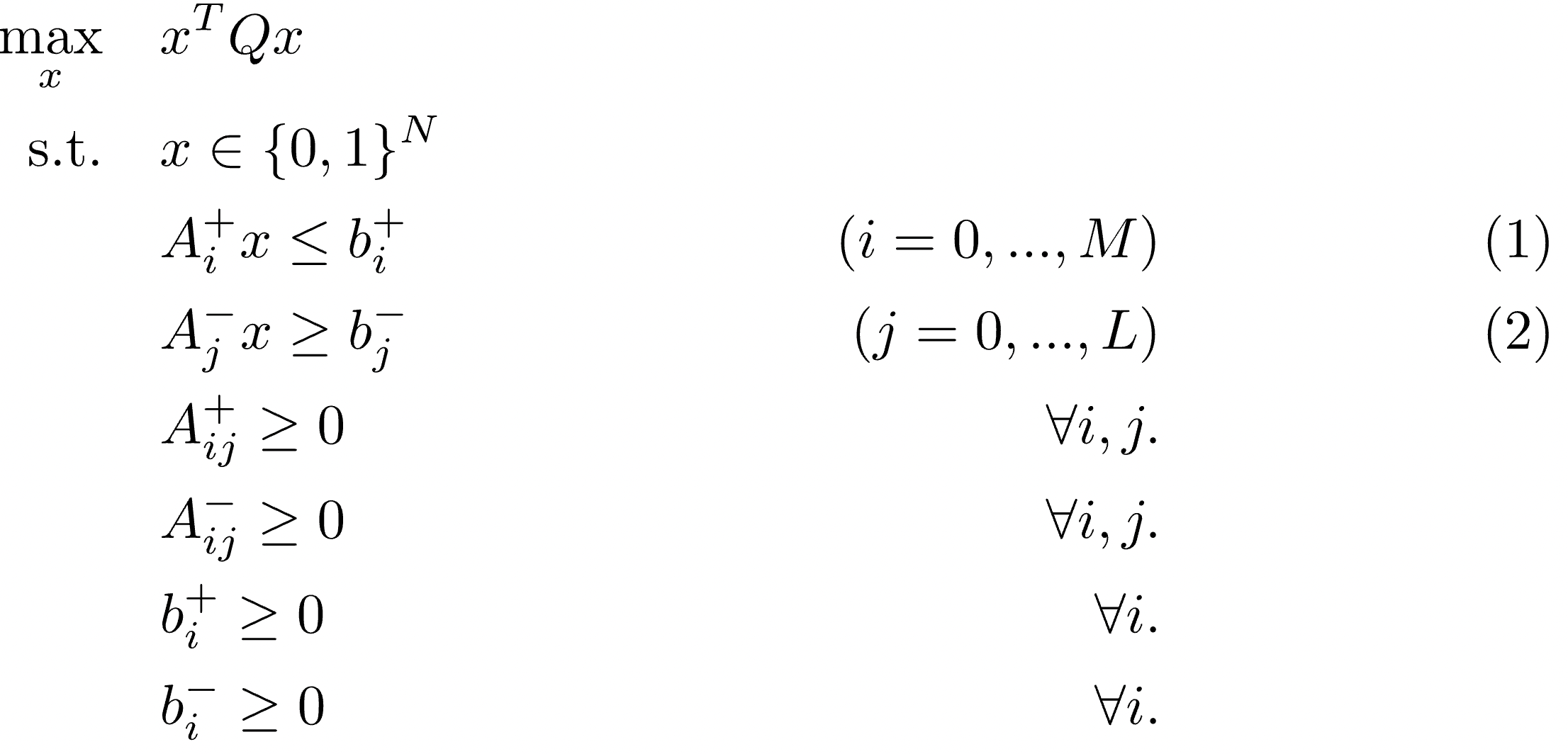Our CorcaOR-Solver-QKP is a tool for solving Quadratic Knapsack Problem in various constraints or environments. We offer two types of solvers for following constraints.
The original paper[1] introduced linear MDMKP solver, which can have Multi-demand(2) and Multi-Dimensional(1) constraints. While reimplementing the algorithm, we accelerated the algorithm on paper using OpenMP and replaced linear objective function with quadratic objective function. As a result, this solver can solve MDMQKP (Multi-Demand Multi-Dimensional Qudratic Knapsack Problem).
We also implemented ACO Solver. It can have Multi-Dimensional(1) constraints and also we modified it to have quadratic objective function. It can solve MDQKP(Multi-Dimensional Quadratic Knapsack Problem). We mainly used paper [2], and we modified it to use Quadratic objective function.
There isn't any common metric that can evaluate our Algorithms. We'll soon release new dataset for our use case. We just used MDMKP dataset to check successful reimplementation of the TSTS.
Here's our benchmark result.
| dataset-100 | TSTS scores | dataset-250 | TSTS scores |
|---|---|---|---|
| 100-5-2-0-0 | 28384 | 250-5-2-0-0 | 78087 |
| 100-5-2-0-1 | 26386 | 250-5-2-0-1 | 74073 |
| 100-5-2-0-2 | 23484 | 250-5-2-0-2 | 69589 |
| 100-5-2-0-3 | 27374 | 250-5-2-0-3 | 80065 |
| 100-5-2-0-4 | 30632 | 250-5-2-0-4 | 70644 |
| 100-5-2-0-5 | 44614 | 250-5-2-0-5 | 126998 |
| 100-5-2-1-0 | 10364 | 250-5-2-1-0 | 26383 |
| 100-5-2-1-1 | 11114 | 250-5-2-1-1 | 26792 |
| 100-5-2-1-2 | 10124 | 250-5-2-1-2 | 27089 |
| 100-5-2-1-3 | 10567 | 250-5-2-1-3 | 26087 |
| 100-5-2-1-4 | 10547 | 250-5-2-1-4 | 27120 |
| 100-5-2-1-5 | 17545 | 250-5-2-1-5 | 44023 |
| 100-5-5-0-0 | 21892 | 250-5-5-0-0 | 68025 |
| 100-5-5-0-1 | 26280 | 250-5-5-0-1 | 60397 |
| 100-5-5-0-2 | 20628 | 250-5-5-0-2 | 62054 |
| 100-5-5-0-3 | 21547 | 250-5-5-0-3 | 66484 |
| 100-5-5-0-4 | 25074 | 250-5-5-0-4 | 61929 |
| 100-5-5-0-5 | 40327 | 250-5-5-0-5 | 127202 |
| 100-5-5-1-0 | 10210 | 250-5-5-1-0 | 26772 |
| 100-5-5-1-1 | 10625 | 250-5-5-1-1 | 26440 |
| 100-5-5-1-2 | 10124 | 250-5-5-1-2 | 26364 |
| 100-5-5-1-3 | 10030 | 250-5-5-1-3 | 25622 |
| 100-5-5-1-4 | 9964 | 250-5-5-1-4 | 25899 |
| 100-5-5-1-5 | 15603 | 250-5-5-1-5 | 40928 |
| 100-10-5-0-0 | 21852 | 250-10-5-0-0 | 56049 |
| 100-10-5-0-1 | 20645 | 250-10-5-0-1 | 59406 |
| 100-10-5-0-2 | 19517 | 250-10-5-0-2 | 54416 |
| 100-10-5-0-3 | 20454 | 250-10-5-0-3 | 51962 |
| 100-10-5-0-4 | 19278 | 250-10-5-0-4 | 57346 |
| 100-10-5-0-5 | 35903 | 250-10-5-0-5 | 98481 |
| 100-10-5-1-0 | 10018 | 250-10-5-1-0 | 26722 |
| 100-10-5-1-1 | 9839 | 250-10-5-1-1 | 26314 |
| 100-10-5-1-2 | 10000 | 250-10-5-1-2 | 25440 |
| 100-10-5-1-3 | 10544 | 250-10-5-1-3 | 26927 |
| 100-10-5-1-4 | 10011 | 250-10-5-1-4 | 26607 |
| 100-10-5-1-5 | 16230 | 250-10-5-1-5 | 46043 |
| 100-10-10-0-0 | 22054 | 250-10-10-0-0 | 52195 |
| 100-10-10-0-1 | 20103 | 250-10-10-0-1 | 53573 |
| 100-10-10-0-2 | 19381 | 250-10-10-0-2 | 46687 |
| 100-10-10-0-3 | 17434 | 250-10-10-0-3 | 54674 |
| 100-10-10-0-4 | 18792 | 250-10-10-0-4 | 49295 |
| 100-10-10-0-5 | 33837 | 250-10-10-0-5 | 92565 |
| 100-10-10-1-0 | 8560 | 250-10-10-1-0 | 26498 |
| 100-10-10-1-1 | 8493 | 250-10-10-1-1 | 25702 |
| 100-10-10-1-2 | 9266 | 250-10-10-1-2 | 26410 |
| 100-10-10-1-3 | 9823 | 250-10-10-1-3 | 26426 |
| 100-10-10-1-4 | 8929 | 250-10-10-1-4 | 26491 |
| 100-10-10-1-5 | 14152 | 250-10-10-1-5 | 42286 |
Because this benchmark only evaluates linear reward, we inserted the reward value to the diagonal part of the reward matrix. Considering the increase of time complexity, the overall result is almost same as the original one.
You can download dataset in https://grafo.etsii.urjc.es/optsicom/binaryss/ .
- Making Wrappers and More general solvers for many cases.
- Lai, Xiangjing & Hao, Jin-Kao & Yue, Dong, 2019. "Two-stage solution-based tabu search for the multidemand multidimensional knapsack problem," European Journal of Operational Research, Elsevier, vol. 274(1), pages 35-48. https://ideas.repec.org/a/eee/ejores/v274y2019i1p35-48.html
- Solnon, Christine and Bridge, Derek, 2006. "An Ant Colony Optimization Meta-Heuristic for Subset Selection Problems," System Engineering using Particle Swarm Optimization, Nova Science publishers, pages 3-25. https://hal.archives-ouvertes.fr/hal-01541555/file/PSO2006.pdf