decision tree algorithm

决策树代码简单实现

---

前言

产生本文的缘由

大三时，居然要来写大一的课设，倒霉透了，简单的又不想写，难点的，也就这个了，唉。

---

以下是本篇文章正文内容

一、决策树例子

1.假设

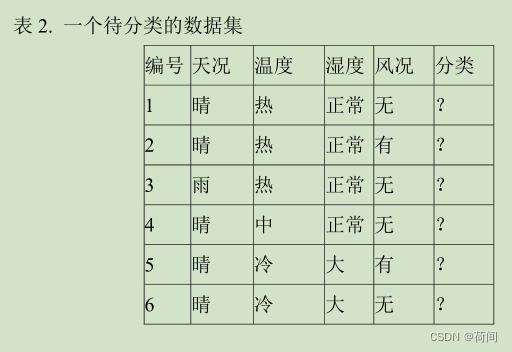
对于一个天气系统，假设我们有天况 温度 湿度 风况 四个参数，每个参数对应于不同的情况。
==天况对应于 晴 多云 雨 晴 多云 雨 分别对应于 1 2 3
分类结果中 Y表示好天气 N表示坏天气==

1	天况  晴  多云  雨   1 2 3
2	温度  热 中  冷      1 2 3
3	湿度  大 正常        1 2
4	风况  无 有          1 2
	分类  N   Y          0 1

2.训练集

对应的数据如下：
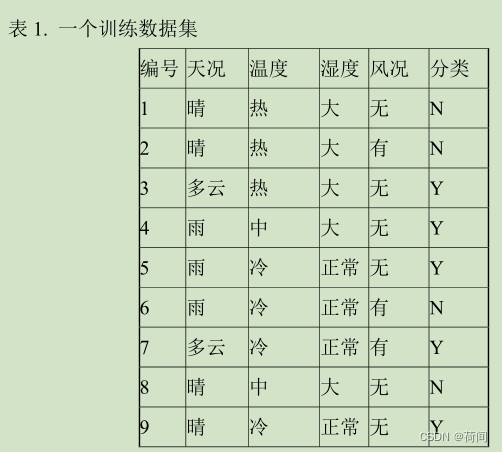
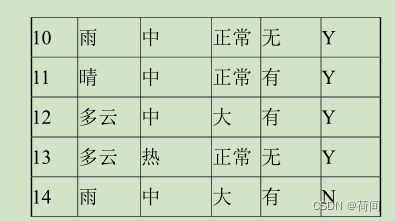
天况 温度 湿度 风况 分类结果==分别对应右侧5列==

data_01:	1	1	1	1	0
data_02:	1	1	1	2	0
data_03:	2	1	1	1	1
data_04:	3	2	1	1	1
data_05:	3	3	2	1	1
data_06:	3	3	2	2	0
data_07:	2	3	2	2	1
data_08:	1	2	1	1	0
data_09:	1	3	2	1	1
data_10:	3	2	2	1	1
data_11:	1	2	2	2	1
data_12:	2	2	1	2	1
data_13:	2	1	2	1	1
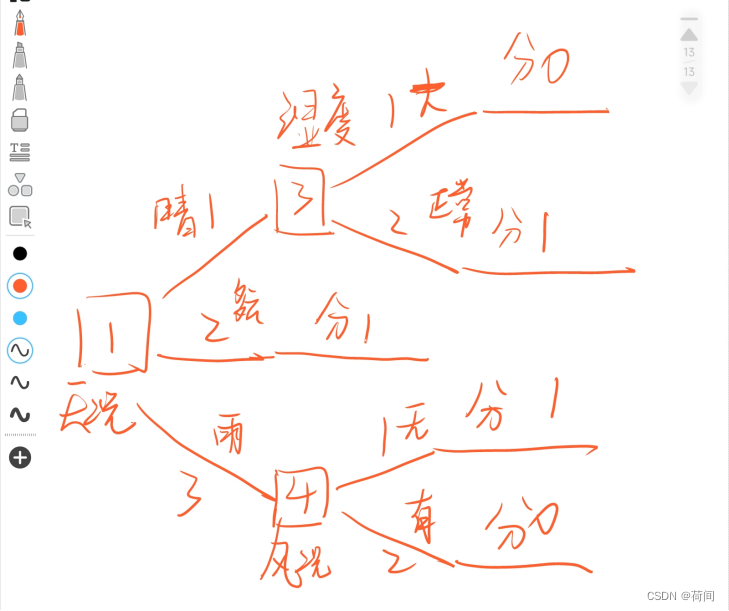
data_14:	3	2	1	2	0

3.决策树

下面就是一颗经过仅仅只有16个样本，训练得到的决策树。

---

4.由决策树进行测试案例

比如说，我们拿训练集的第一条数据进行测试： 首先，根节点是1，就看天况，是晴天 那么就从==1号节点，由分支1，走到3号节点==

然后，此时的根节点是3，就看湿度，是大 那么就从==3号节点，由分支1，找到分类结果0，也就是分类为N==

可以看出，咱的决策树很牛逼，分类是正确的。

---

二、关键公式和代码

1.原理

原理
决策树通过使用称为 信息增益的统计属性 来决定当前节点的最佳属性。
增益是衡量给定属性将训练示例分离到各自目标类的程度。
增益最高的被选中，增益越高，树就越短。
为了定义增益，首先定义熵。
熵是属性中可用信息量的度量。

2.熵

公式 Entropy(S) = - ∑ ( p(i) * log2 p(i) )

代码实现

// 返回与特定属性的给定attrval匹配的行数
// 例如 v是数据集 attrnum 是天况  	attrval 是 天况可能的类型 晴
vector<vector<int>> newDataSet(vector<vector<int>> &v, int attrnum, int attrval)
{
	vector<vector<int>> dstemp;
	for (int i = 0; i < v.size(); ++i)
	{
		if (v[i][attrnum] == attrval)
		{
			dstemp.push_back(v[i]); // 保存对应的训练项
		}
	}
	return dstemp;
}

// 计算一个特定集合的熵
// Entropy(S) =  - ∑ (p(i) * log2 p(i))    i~[0-1],两种分类情况
float calcEntropy(vector<vector<int>> &v)
{

	float e = 0;
	// 在v初始化的时候，v[0]表示分类
	// newDataSet(v, 0, 0),其实是对应于newDataSet(v, 分类 , 0)
	float a0 = newDataSet(v, 0, 0).size(); // 后续计算(p(0) * log2 p(0))中的p0的分子 ， 表示v中分类为0的项数

	// newDataSet(v, 0, 1),其实是对应于newDataSet(v, 分类 , 1)
	float a1 = newDataSet(v, 0, 1).size(); // 后续计算(p(1) * log2 p(1))中的p1的分子 ， 表示v中分类为1的项数

	//一般情况下 a0 + a1 == v.size()
	if (a0 == 0 || a1 == 0)
		return 0;
	e = -(((a0 / v.size()) * (log(a0 / v.size()) / log(2))) + ((a1 / v.size()) * (log(a1 / v.size()) / log(2))));
	return e; // Entropy(S) =  - ∑ (p(i) * log2 p(i))
}

3.增益

公式 Gain(S, A) = Entropy(S) - ∑((|Sv| / |S|) * Entropy(Sv)

代码实现

float calcGain(vector<vector<int>> &v, int attrnum)
{
	float g;
	float calc = 0;
	vector<vector<int>> ds1;
	for (int i = 1; i <= attrs_new[attrnum].size(); ++i)
	{
		// ds1中包含了传过来的训练集中v的所有与attrnum相关的i的属性的训练项
		/*
		例如：
			newDataSet(v, 1 , 1)
			即为
			newDataSet(v, 天况 , 1)

			下面是传过来的v
			分类 天况 温度 湿度 风况
			0	1	1	1	1
			0	1	1	1	2
			1	2	1	1	1

			那么ds1就是只包含下面两项，因为天况对应的第三项是2，不是1
			0	1	1	1	1
			0	1	1	1	2
		*/
		ds1 = newDataSet(v, attrnum, i); // Sv
		float gaina = ds1.size();		 //   |Sv|
		float ab = calcEntropy(ds1);	 //  Entropy(Sv)
		calc += (gaina / v.size()) * ab; // ∑((|Sv| / |S|) * Entropy(Sv)
	}
	g = calcEntropy(v) - calc; // Gain(S, A) = Entropy(S) - ∑((|Sv| / |S|) * Entropy(Sv)
	return g;
}

三、决策树超形象示例

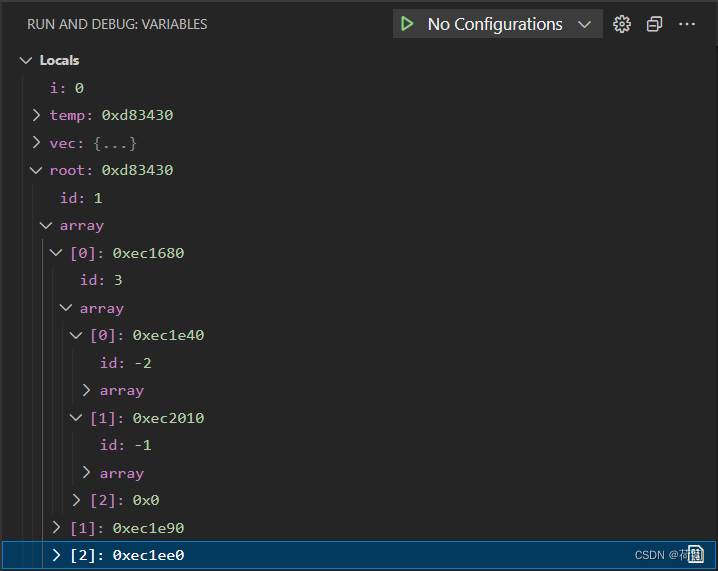
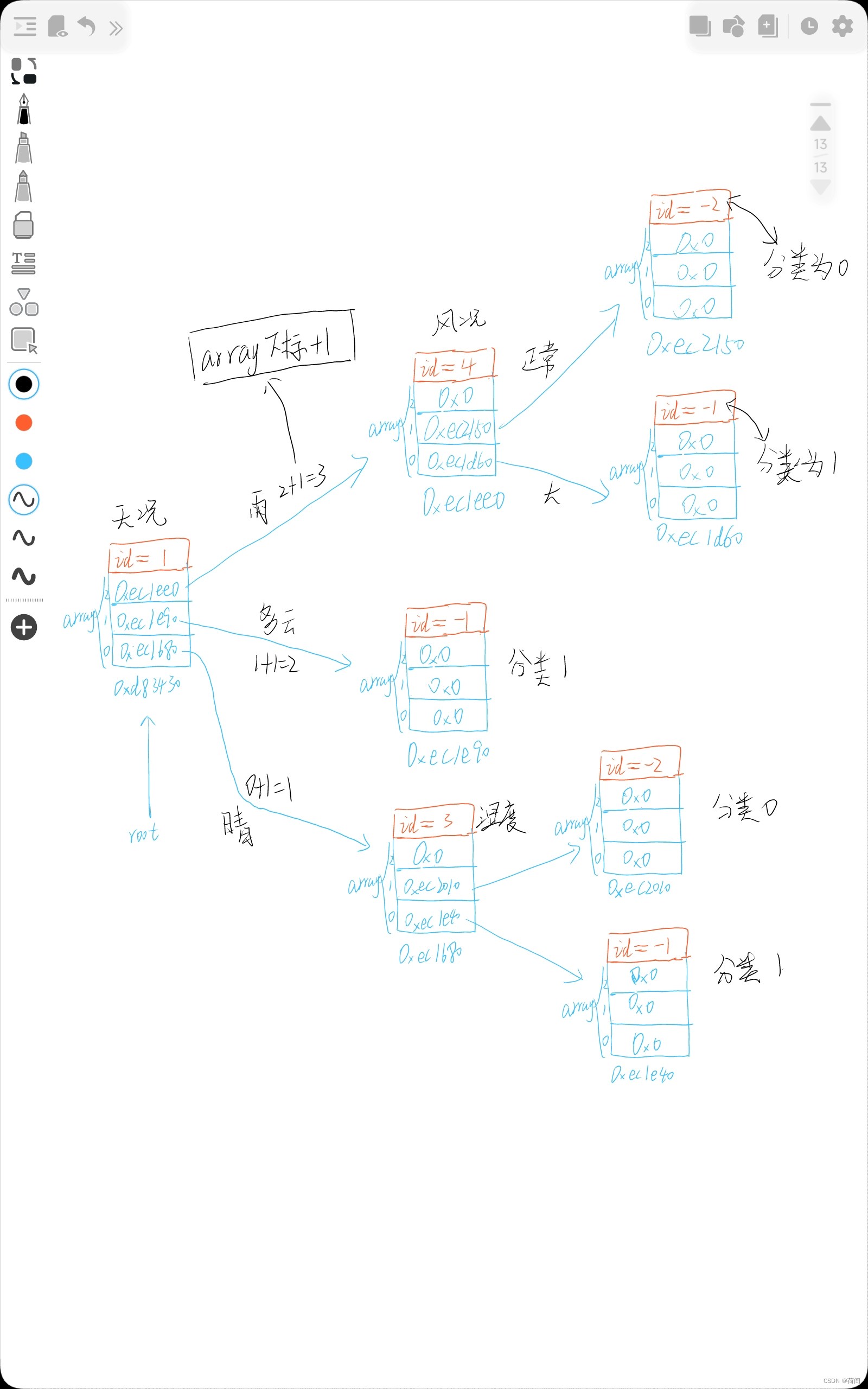
如下图，很清晰

四、决策树预测

预测初始文件：

 与 测试集的文件输入到二维向量中类似，但是predictingdata.txt中的分类结果默认为N，
 也就是最右边的列全0，后期调用predict函数预测时，写入到output-pre.txt文件中

data_01:	1	1	2	1	0
data_02:	1	1	2	2	0
data_03:	3	1	2	1	0
data_04:	1	2	2	1	0
data_05:	1	3	1	2	0
data_06:	1	3	1	1	0

成功预测文件：

data_01:	1	1	2	1	Y
data_02:	1	1	2	2	Y
data_03:	3	1	2	1	Y
data_04:	1	2	2	1	Y
data_05:	1	3	1	2	N
data_06:	1	3	1	1	N