Thinking Functionally: Mathematical functions

The impetus behind functional programming comes from mathematics. Mathematical functions have a number of very nice features that functional languages try to emulate in the real world.

So first, let’s start with a mathematical function that adds 1 to a number.

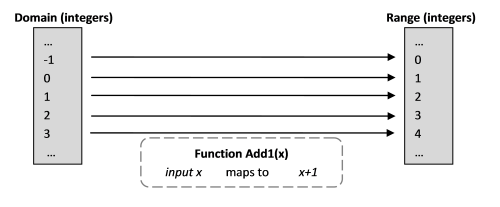
Add1(x) = x+1

What does this really mean? Well it seems pretty straightforward. It means that there is an operation that starts with a number, and adds one to it.

Let’s introduce some terminology:

• The set of values that can be used as input to the function is called the domain. In this case, it could be the set of real numbers, but to make life simpler for now, let’s restrict it to integers only.
• The set of possible output values from the function is called the range (technically, the image on the codomain). In this case, it is also the set of integers.
• The function is said to map the domain to the range.

Here’s how the definition would look in C#

    static int Add1(int x) => x + 1;

Let’s look at that output in detail:

• The overall meaning is “the function Add1 maps integers (the domain) onto integers (the range)”.
• Add1 is defined as a “val”, short for "value". Hmmm… what does that mean? We’ll discuss values shortly.
• We talk about functions using arrow notation: int -> int. The arrow notation -> is used to show the domain and range. In this case, the domain is the int on the left hand side of the arrow, and the range is the int to the right hand side of the arrow. This can be seen in the Func type representation: Func<int, int>.

The (int x) is the domain, and the int to the left hand side of Add1 is the range. In this case, the domain is the int type, and the range is also the int type. Although you could argue that (int x) represents a single-item tuple of int.

Also note that the type (int) was specified; can this be generalised? Yes. We'll revisit that later.

Key properties of mathematical functions

Mathematical functions have some properties that are very different from the kinds of functions you are used to in procedural programming.

• A function always gives the same output value for a given input value
• A function has no side effects.

These properties provide some very powerful benefits, and so functional programming languages try to enforce these properties in their design as well. Let's look at each of them in turn.

Mathematical functions always give the same output for a given input

In imperative programming, we think that functions "do" something or "calculate" something. A mathematical function does not do any calculation – it is purely a mapping from input to output. In fact, another way to think of defining a function is simply as the set of all the mappings. For example, in a very crude way we could define the Add1 function (in C#) as

int Add1(int input)
{ 
   switch (input)
   {
       case 0: return 1;
       case 1: return 2;
       case 2: return 3;
       case 3: return 4;
       etc ad infinitum
   }
}

Obviously, we can't have a case for every possible integer, but the principle is the same. You can see that absolutely no calculation is being done at all, just a lookup.

Mathematical functions are free from side effects

In a mathematical function, the input and the output are logically two different things, both of which are predefined. The function does not change the input or the output -- it just maps a pre-existing input value from the domain to a pre-existing output value in the range.

In other words, evaluating the function cannot possibly have any effect on the input, or anything else for that matter. Remember, evaluating the function is not actually calculating or manipulating anything; it is just a glorified lookup.

This "immutability" of the values is subtle but very important. If I am doing mathematics, I do not expect the numbers to change underneath me when I add them! For example, if I have:

    x = 5
    y = x+1

I would not expect x to be changed by the adding of one to it. I would expect to get back a different number (y) and x would be left untouched. In the world of mathematics, the integers already exist as an unchangeable set, and the Add1 function simply defines a relationship between them.

The power of pure functions

The kinds of functions which have repeatable results and no side effects are called "pure functions", and you can do some interesting things with them:

• They are trivially parallelisable. I could take all the integers from 1 to 1000, say, and given 1000 different CPUs, I could get each CPU to execute the Add1 function for the corresponding integer at the same time, safe in the knowledge that there was no need for any interaction between them. No locks, mutexes, semaphores, etc., needed.
• I can use a function lazily, only evaluating it when I need the output. I can be sure that the answer will be the same whether I evaluate it now or later.
• I only ever need to evaluate a function once for a certain input, and I can then cache the result, because I know that the same input always gives the same output.
• If I have a number of pure functions, I can evaluate them in any order I like. Again, it can't make any difference to the final result.

So you can see that if we can create pure functions in a programming language, we immediately gain a lot of powerful techniques. And indeed you can do all these things in C#:

"Unhelpful" properties of mathematical functions

Mathematical functions also have some properties that seem not to be very helpful when used in programming.

• The input and output values are immutable
• A function always has exactly one input and one output

These properties are mirrored in the design of functional programming languages too. Let's look at each of these in turn.

The input and output values are immutable

Immutable values seem like a nice idea in theory, but how can you actually get any work done if you can't assign to variables in a traditional way?

I can assure you that this is not as much as a problem as you might think. As you work through this series, you'll see how this works in practice.

Mathematical functions always have exactly one input and one output

As you can see from the diagrams, there is always exactly one input and one output for a mathematical function. This is true for functional programming languages as well, although it may not be obvious when you first use them.

That seems like a big annoyance. How can you do useful things without having functions with two (or more) parameters?

Well, it turns there is a way to do it: it is called "currying" and it deserves its own post, which is coming up soon.

In fact, as you will later discover, these two "unhelpful" properties will turn out to be incredibly useful and a key part of what makes functional programming so powerful.

NEXT: Function Values