Weighting
Every concept and their ancestors are weighted.
The weights can be given in the abundances and ref_abundances parameters.
If no weights are given as input parameter, all input concepts will be weighted by default to 1
(input weight).
All the ancestors retreived not given as input are weighted to 0 (input weight).
The weights are cumulative, each weight of a concept is equal to the sum of the weights of its uniques initially weighted children (calculated weight).
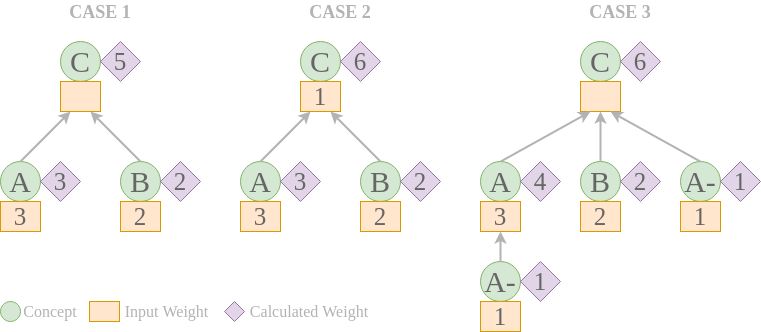
Input
- A has as parents C
- A has as input weight 3
- B has as parents C
- B has as input weight 2
Finality
- Then C has as calculated weight 3+2=5
Input
- A has as parents C
- A has as input weight 3
- B has as parents C
- B has as input weight 2
- C has as input weight 1
Finality
- Then C has as calculated weight 3+2+1=6
Input
- A has as parents C
- A has as input weight 3
- B has as parents C
- B has as input weight 2
- A- has as parents A
- A- has as parents C
- A- has as input weight 1
Finality
- Then A has as calculated weight 3+1=4
- Then C has as calculated weight 3+2+1=6 (A- counted only once)
The calculated weight is used to calculate the sectors size (and the colorization for topology analysis).
Sectors size are proportions calculated in 2 different ways. For a given concept sector :
- If the sum of the sectors children proportions <= sector proportion :
- Then sector's children proportions are unchanged
- Else :
- Then sector's children proportions are recalculated so that the sum of their proportion is equal to sector's proportion.
Input
- A has as parents C
- A has as proportion 0.3
- B has as parents C
- B has as proportion 0.2
- C has as proportion 0.6
Finality
- 0.2+0.3 < 0.6
- Then C has as size 0.6
- Then A has as size 0.3
- Then B has as size 0.2
Input
- A has as parents C
- A has as proportion 0.3
- B has as parents C
- B has as proportion 0.2
- C has as proportion 0.5
Finality
- 0.2+0.3 = 0.5
- Then C has as size 0.5
- Then A has as size 0.3
- Then B has as size 0.2
Input
- A has as parents C
- A has as proportion 0.75
- B has as parents C
- B has as proportion 0.25
- C has as proportion 0.8
Finality
- 0.75+0.25 > 0.8
- Then C has as size 0.8
- Then A has as size 0.6 :
${0.75 \over {0.75+0.25}} \times 0.8$ - Then B has as size 0.2 :
${0.25 \over {0.75+0.25}} \times 0.8$
The re-calculation can cause visual delusions on the figure. Per exemple if the root R (proportion 1) has 3 children : A, B and C with each a proportion of 0.5, the figure will show three sectors under the root with a ratio at 33.3% (instead of 50%).
In this case the colorization in topology analysis can help to compare sectors proportions.
This situation can happen in cases where the ontology has concepts with more than 1 parent.