ProbeScan

ProbeScan performs the actual scanning procedure. It implements the algorithm to rasterize the semi-classical limit of the brane configuration defined by a set of matrices as submanifold of the target space 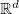. For more information, see the paper containing the theoretical background.

The quality of the scans produced by ProbeScan can be vastly improved by manually adjusting certain parameters. A useful starting point to look for ways to focus and improve ProbeScan's performance is using ProbeDirectionalScan to 'test the waters', so to speak, and then use information obtained from that initial naive scan and feed it into ProbeScan via ProbeReset.

How to use `ProbeScan`

ProbeScan can be used like any other function in Mathematica once the BProbe package has been installed and initialized in a given notebook.

Since ProbeScan might need quite a lot of time to finish its calculation, it would be quite bothersome to always wait for it to finish and only afterwards check the data to perhaps find out that the whole calculation did not make much sense due to some mistakes in the starting values or chosen parameters.

To resolve this issue, the package remembers the current state of the calculation independent of the state of ProbeScan. In practice, this means you can start the calculation by calling ProbeScan and then abort the procedure in Mathematica (e.g. via the key combination [Alt] + [.]) at any time in order to later resume it with the same call ProbeScan (killing the local kernel will of course reset the calculation).

Of course, this immediately raises the question, how to start a completely new calculation. This is done using ProbeReset, or simply by reinitializing the whole package with ProbeInit.

During the calculation, its progress is indicated by the Mathematica-Monitor function. It always shows you:

the number of already gathered points,
the number of points which are in the queue for processing.

and optionally it can also show you:

the number of points rejected due to certain restrictions set via [options].
the largest 'small' eigenvalue emerging during the calculation,
the largest energy-gradient emerging during the calculation,
the largest energy value emerging during the calculation.

Options

ProbeScan admits the following options:

Options	Description
`StepSize`	The step size is a number which directly influences the resolution of the rasterized manifold. On the one hand, it has to be sufficiently small to get a "good" approximation to the semi-classical limit as manifold. On the other hand, it has to be large enough to be computationally manageable. [The computational effort grows with (1/s)^n where s is the step size and n the dimension of the manifold.] This option overrides the default guess of `ProbeInit`. Example: `StepSize->0.1`
`Dimension`	The dimension of the semi-classical limit as manifold. This number has to be decided on the given hierarchy of eigenvalues of the Hesse matrix at the starting point. The number of "small" eigenvalues corresponds to the dimension. If the default guess of `ProbeInit` was not satisfactory, you can choose to override this guess with this option. Example: `Dimension->2`
`ReplacePoints`	The scanning algorithm replaces each new point by its corresponding location expectation value in each step. In some cases, this improves the quality significantly. If this is switched on, in a lot of cases, the next four options are not needed to produce a reasonable result. Default: `True` Example: `ReplacePoints->False`
`MinimalSurface`	If one is lucky, the whole manifold is a "minimal surface" (of the displacement energy). In this case, one can significantly enhance the quality of the rasterized manifold by specifying `MinimalSurface->True`. Then the next three options become mostly irrelevant. Note, however, that this comes with a significant performance loss. Default: `False` Example: `MinimalSurface->True`
`MaxEnergy`	If this value is set, the procedure only collects points whose displacement energy is below this number. Default: ∞ Example: `MaxEnergy->2.1`
`MaxEV`	The whole procedure does not make sense any more if the hierarchy of the Hesse matrix eigenvalues has broken down. The largest allowed "small" eigenvalue for collected points can be set with this option. Default: ∞ Example: `MaxEV->0.01`
`MaxGradient`	On the semi-classical manifold, one expects the gradient to point in the tangential directions. This option allows to set the maximal allowed magnitude of the "transversal" component of the gradient. "Transversal" here means to be orthogonal to the plane spanned by the Hesse-Matrix eigenvectors corresponding to the 'small' eigenvalues. Note, that setting this option comes with a significant performance cost. Default: ∞ Example: `MaxGradient->0.3`
`EnergyTracker`	Setting this option to `True` enables the status information panel to show the largest displacement energy value emerging during the calculation. The performance cost should be marginal in most cases. Default: `False` Example: `EnergyTracker->True`
`EVTracker`	Setting this option to `True` enables the status information panel to show the largest "small" eigenvalue emerging during the calculation. The performance cost should be marginal in most cases. Default: `False` Example: `EVTracker->True`
`GradientTracker`	Setting this option to `True` enables the status information panel to show the largest "transveral" component of displacement energy gradient emerging during the calculation. Beware that the performance cost is not neglectible in most cases. Default: `False` Example: `GradientTracker->True`
`UpdateInterval`	Sets the update interval of the status information panel in seconds. This value shouldn't be chosen too small since it could negatively influence performance. The default value should serve you well in this regard. Default: `0.1` Example: `UpdateInterval->0.5`

Examples

Fuzzy 2-sphere

<< BProbeM`

t = PauliMatrix[{1,2,3}];
ProbeInit[t];
ProbeScan[MinimalSurface->True];

The first three calls are familiar from our first example. The last call takes a few seconds while it calculates a point cloud corresponding to the semi-classical limit of the fuzzy brane defined by the 3 Pauli matrices.

See ProbeGetPoints for information on how to retrieve this point cloud.

The result will be an approximation to the unit sphere embedded in R^3.